
【题目】已知函数f(x)=x2+2ax+3在(﹣∞,1]上是减函数,当x∈[a+1,1]时,f(x)的最大值与最小值之差为g(a),则g(a)的最小值是 .
【答案】1
【解析】解:解:∵f(x)在(﹣∞,1]上是减函数, ∴﹣a≥1,即a≤﹣1.
∴f(x)在[a+1,1]上的最大值为f(a+1)=3a2+4a+4,
最小值为f(1)=4+2a,
∴g(a)=3a2+2a=3(a+ ![]() )2﹣
)2﹣ ![]() ,
,
∴g(a)在(﹣∞,﹣1]上单调递减,
∴g(a)的最小值为g(﹣1)=1.
所以答案是:1.
【考点精析】通过灵活运用函数的最值及其几何意义和二次函数的性质,掌握利用二次函数的性质(配方法)求函数的最大(小)值;利用图象求函数的最大(小)值;利用函数单调性的判断函数的最大(小)值;当![]() 时,抛物线开口向上,函数在
时,抛物线开口向上,函数在![]() 上递减,在
上递减,在![]() 上递增;当
上递增;当![]() 时,抛物线开口向下,函数在
时,抛物线开口向下,函数在![]() 上递增,在
上递增,在![]() 上递减即可以解答此题.
上递减即可以解答此题.


 新课标快乐提优暑假作业陕西旅游出版社系列答案
新课标快乐提优暑假作业陕西旅游出版社系列答案 暑假衔接培优教材浙江工商大学出版社系列答案
暑假衔接培优教材浙江工商大学出版社系列答案科目:高中数学 来源: 题型:
【题目】设甲、乙两人每次射击命中目标的概率分别为 ![]() ,且各次射击相互独立,若按甲、乙、甲、乙…的次序轮流射击,直到有一人击中目标就停止射击,则停止射击时,甲射击了两次的概率是( )
,且各次射击相互独立,若按甲、乙、甲、乙…的次序轮流射击,直到有一人击中目标就停止射击,则停止射击时,甲射击了两次的概率是( )
A.![]()
B.![]()
C.![]()
D.![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知F1 , F2分别是双曲线 ![]() =1(a>0,b>0)的左,右焦点,点F1关于渐近线的对称点恰好在以F2为圆心,|OF2|(O为坐标原点)为半径的圆上,则该双曲线的离心率为 .
=1(a>0,b>0)的左,右焦点,点F1关于渐近线的对称点恰好在以F2为圆心,|OF2|(O为坐标原点)为半径的圆上,则该双曲线的离心率为 .
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】给出下列命题中
① 非零向量![]() 满足
满足![]() ,则
,则![]() 的夹角为
的夹角为![]() ;
;
② ![]()
![]() >0是
>0是![]() 的夹角为锐角的充要条件;
的夹角为锐角的充要条件;
③若![]() 则
则![]() 必定是直角三角形;
必定是直角三角形;
④△ABC的外接圆的圆心为O,半径为1,若![]() ,且
,且![]() ,则向量
,则向量![]() 在向量
在向量![]() 方向上的投影为
方向上的投影为![]() .
.
以上命题正确的是 __________ (注:把你认为正确的命题的序号都填上)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】双十一网购狂欢,快递业务量猛增.甲、乙两位快递员![]() 月
月![]() 日到
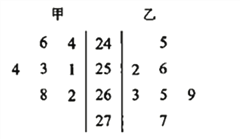
日到![]() 日每天送件数量的茎叶图如图所示.
日每天送件数量的茎叶图如图所示.
(Ⅰ)根据茎叶图判断哪个快递员的平均送件数量较多(写出结论即可);
(Ⅱ)求甲送件数量的平均数;
(Ⅲ)从乙送件数量中随机抽取![]() 个,求至少有一个送件数量超过甲的平均送件数量的概率.
个,求至少有一个送件数量超过甲的平均送件数量的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】定义在R上的函数f(x)的图象关于点(﹣ ![]() ,0)成中心对称,且对任意的实数x都有
,0)成中心对称,且对任意的实数x都有 ![]() ,f(﹣1)=1,f(0)=﹣2,则f(1)+f(2)+…+f(2 017)=( )
,f(﹣1)=1,f(0)=﹣2,则f(1)+f(2)+…+f(2 017)=( )
A.0
B.﹣2
C.1
D.﹣4
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数 ![]() .任取t∈R,若函数f(x)在区间[t,t+1]上的最大值为M(t),最小值为m(t),记g(t)=M(t)﹣m(t).
.任取t∈R,若函数f(x)在区间[t,t+1]上的最大值为M(t),最小值为m(t),记g(t)=M(t)﹣m(t).
(1)求函数f(x)的最小正周期及对称轴方程;
(2)当t∈[﹣2,0]时,求函数g(t)的解析式;
(3)设函数h(x)=2|x﹣k|,H(x)=x|x﹣k|+2k﹣8,其中实数k为参数,且满足关于t的不等式 ![]() 有解,若对任意x1∈[4,+∞),存在x2∈(﹣∞,4],使得h(x2)=H(x1)成立,求实数k的取值范围.
有解,若对任意x1∈[4,+∞),存在x2∈(﹣∞,4],使得h(x2)=H(x1)成立,求实数k的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com