
【题目】海水养殖场进行某水产品的新、旧网箱养殖方法的产量对比,收获时各随机抽取了100个网箱,测量各箱水产品的产量(单位:kg),其频率分布直方图如下:

(1)根据箱产量的频率分布直方图填写下面![]() 列联表,从等高条形图中判断箱产量是否与新、旧网箱养殖方法有关;
列联表,从等高条形图中判断箱产量是否与新、旧网箱养殖方法有关;
(2)根据列联表判断是否有99%的把握认为箱产量与养殖方法有关?
箱产量<50kg | 箱产量≥50kg | |
旧养殖法 | ||
新养殖法 |
参考公式:
(1)给定临界值表
P(K | 0.50 | 0.40 | 0.25 | 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| 0.455 | 0.708 | 1.323 | 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
(2)![]() 其中
其中![]() 为样本容量.
为样本容量.
科目:高中数学 来源: 题型:
【题目】某地举办科技博览会,有![]() 个场馆,现将
个场馆,现将![]() 个志愿者名额分配给这
个志愿者名额分配给这![]() 个场馆,要求每个场馆至少有一个名额且各场馆名额互不相同的分配方法共有( )种
个场馆,要求每个场馆至少有一个名额且各场馆名额互不相同的分配方法共有( )种
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,某运动员从A市出发沿海岸一条笔直公路以每小时15km的速度向东进行长跑训练,长跑开始时,在A市南偏东方向距A市75km,且与海岸距离为45km的海上B处有一艘划艇与运动员同时出发,要追上这位运动员.

(1)划艇至少以多大的速度行驶才能追上这位运动员?
(2)求划艇以最小速度行驶时的行驶方向与![]() 所成的角.
所成的角.
(3)若划艇每小时最快行驶11.25km,划艇全速行驶,应沿何种路线行驶才能尽快追上这名运动员,最快需多长时间?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图![]() ,在矩形
,在矩形![]() 中,
中, ![]() ,
, ![]() 为
为![]() 的中点,
的中点, ![]() 为
为![]() 的中点.将
的中点.将![]() 沿
沿![]() 折起到
折起到![]() ,使得平面
,使得平面![]() 平面
平面![]() (如图
(如图![]() ).
).


图1 图2
(Ⅰ)求证: ![]() ;
;
(Ⅱ)求直线![]() 与平面
与平面![]() 所成角的正弦值;
所成角的正弦值;
(Ⅲ)在线段![]() 上是否存在点
上是否存在点![]() ,使得
,使得![]() 平面
平面![]() ?若存在,求出
?若存在,求出![]() 的值;若不存在,请说明理由.
的值;若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
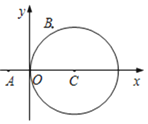
【题目】如图,在平面直角坐标系xOy中,已知圆C:x2+y2-4x=0及点A(-1,0),B(1,2)
(1)若直线l平行于AB,与圆C相交于M,N两点,MN=AB,求直线l的方程;
(2)若圆C上存在两个点P,使得PA2+PB2=a(a>4),求a的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com