
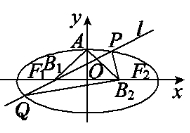
【题目】如图,设椭圆的中心为原点O,长轴在x轴上,上顶点为A,左、右焦点分别为F1,F2,线段OF1,OF2的中点分别为B1,B2,且△AB1B2是面积为4的直角三角形.过B1作l交椭圆于P、Q两点,使PB2垂直QB2,求直线l的方程__________.
【答案】x+2y+2=0和x-2y+2=0
【解析】
试题分析:设所求椭圆的标准方程为![]() (a>b>0),右焦点为F2(c,0).
(a>b>0),右焦点为F2(c,0).
因△AB1B2是直角三角形,又|AB1|=|AB2|,故∠B1AB2为直角,因此|OA|=|OB2|,得b=![]() .结合c2=a2-b2得4b2=a2-b2,故a2=5b2,c2=4b2,所以离心率e=
.结合c2=a2-b2得4b2=a2-b2,故a2=5b2,c2=4b2,所以离心率e=![]() =
=![]() .
.
在Rt△AB1B2中,OA⊥B1B2,故
S△AB1B2=![]() ·|B1B2|·|OA|=|OB2|·|OA|=
·|B1B2|·|OA|=|OB2|·|OA|=![]() ·b=b2.
·b=b2.
由题设条件S△AB1B2=4,得b2=4,从而a2=5b2=20.
因此所求椭圆的标准方程为:![]() .
.
![]() ,
,![]() 。由题意知直线l的倾斜角不为0,故可设直线的方程为:
。由题意知直线l的倾斜角不为0,故可设直线的方程为: ![]() 。
。
代入椭圆方程得![]() 。
。
设![]() ,
,![]() ,则
,则 ![]() 是上面方程的两根,因此,
是上面方程的两根,因此,![]() 。又,
。又,![]() ,所以由
,所以由 ![]() ,得
,得 ![]() ,即
,即 ![]() ,解得
,解得![]() 。所以满足条件的直线有两条,其方程分别为
。所以满足条件的直线有两条,其方程分别为![]() 和
和![]() 。
。


科目:高中数学 来源: 题型:
【题目】铁矿石A和B的含铁率为![]() ,冶炼每万吨铁矿石CO2的排放量b及每万吨铁矿石
,冶炼每万吨铁矿石CO2的排放量b及每万吨铁矿石
的价格c如下表:
| b(万吨) |
| |
A | 50% | 1 | 3 |
B | 70% | 0.5 | 6 |
某冶炼厂至少要生产1.9(万吨)铁,若要求CO2的排放量不超过2(万吨),则购买铁矿石的最少费用为________ (百万元).
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,某企业的两座建筑物AB,CD的高度分别为20m和40m,其底部BD之间距离为20m.为响应创建文明城市号召,进行亮化改造,现欲在建筑物AB的顶部A处安装一投影设备,投影到建筑物CD上形成投影幕墙,既达到亮化目的又可以进行广告宣传.已知投影设备的投影张角∠EAF为![]() ,投影幕墙的高度EF越小,投影的图像越清晰.设投影光线的上边沿AE与水平线AG所成角为α,幕墙的高度EF为y(m).
,投影幕墙的高度EF越小,投影的图像越清晰.设投影光线的上边沿AE与水平线AG所成角为α,幕墙的高度EF为y(m).
(1)求y关于α的函数关系式![]() ,并求出定义域;
,并求出定义域;
(2)当投影的图像最清晰时,求幕墙EF的高度.

查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知圆N经过点A(3,1),B(﹣1,3),且它的圆心在直线3x﹣y﹣2=0上.
(1)求圆N的方程;
(2)若点D为圆N上任意一点,且点C(3,0),求线段CD的中点M的轨迹方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】从![]() 中这
中这![]() 个数中取
个数中取![]() 个数组成递增等差数列,所有可能的递增等差数列这个数记为
个数组成递增等差数列,所有可能的递增等差数列这个数记为![]() .
.
(1)当![]() 时,写出所有可能的递增等差数列及
时,写出所有可能的递增等差数列及![]() 的值;
的值;
(2)求![]() ;
;
(3)求证:![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】市场上有一种新型的强力洗衣粉,特点是去污速度快,已知每投放![]() (
(![]() 且
且![]() )个单位的洗衣粉液在一定量水的洗衣机中,它在水中释放的浓度
)个单位的洗衣粉液在一定量水的洗衣机中,它在水中释放的浓度![]() (克/升)随着时间
(克/升)随着时间![]() (分钟)变化的函数关系式近似为
(分钟)变化的函数关系式近似为![]() ,其中
,其中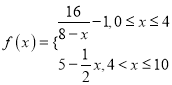 ,若多次投放,则某一时刻水中的洗衣液浓度为每次投放的洗衣液在相应时刻所释放的浓度之和,根据经验,当水中洗衣液的浓度不低于4(克/升)时,它才能起有效去污的作用.
,若多次投放,则某一时刻水中的洗衣液浓度为每次投放的洗衣液在相应时刻所释放的浓度之和,根据经验,当水中洗衣液的浓度不低于4(克/升)时,它才能起有效去污的作用.
(1)若只投放一次4个单位的洗衣液,则有效去污时间可能达几分钟?
(2)若先投放2个单位的洗衣液,6分钟后投放![]() 个单位的洗衣液,要使接下来的4分钟中能够持续有效去污,试求
个单位的洗衣液,要使接下来的4分钟中能够持续有效去污,试求![]() 的最小值(精确到0.1,参考数据:
的最小值(精确到0.1,参考数据: ![]() 取
取![]() ).
).
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在如图所示的圆锥中,OP是圆锥的高,AB是底面圆的直径,点C是弧AB的中点,E是线段AC的中点,D是线段PB的中点,且PO=2,OB=1.

(1)试在PB上确定一点F,使得EF∥面COD,并说明理由;
(2)求点![]() 到面COD的距离.
到面COD的距离.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=![]() ,其中0<a<1,k∈R。
,其中0<a<1,k∈R。
(Ⅰ)若k=1,求函数f(x)的定义域;
(Ⅱ)若a=![]() ,且f(x)在[1,+∞)内总有意义,求k的取值范围。
,且f(x)在[1,+∞)内总有意义,求k的取值范围。
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com