
【题目】已知函数f(x)=(ax﹣1)e2x+x+1(其中e为自然对数的e底数).
(1)若a=0,求函数f(x)的单调区间;
(2)对x∈(0,+∞),f(x)>0恒成立,求a的取值范围.
【答案】
(1)解:a=0时,f(x)=﹣e2x+x+1,f′(x)=﹣2e2x+1,
由f′(x)=0,解得x=﹣ ![]() ,
,
当x∈(﹣∞,﹣ ![]() )时,f′(x)>0,当x∈(﹣
)时,f′(x)>0,当x∈(﹣ ![]() ,+∞)时,f′(x)<0,
,+∞)时,f′(x)<0,
∴函数f(x)的单调增区间为(﹣∞,﹣ ![]() ),单调减区间为(﹣
),单调减区间为(﹣ ![]() ,+∞).
,+∞).
(2)解:f′(x)=(2ax﹣2+a)e2x+1,令g(x)=(2ax﹣2+a)e2x+1,
则g′(x)=4(ax﹣1+a)e2x,
①若a≥1,当x∈(0,+∞),g′(x)>0,从而g(x)在(0,+∞)上单调递增且g(0)=a﹣1≥0,
∴x∈(0,+∞)时,g(x)>0即f′(x)>0,从而f(x)在(0,+∞)上单调递增且f(0)=0,
∴x∈(0,+∞)时,f(x)>0恒成立,符合题意.
②若a≤0,则x∈(0,+∞)时,g′(x)<0恒成立,
∴g(x)在(0,+∞)单调递减,则g(x)<g(0)=a﹣1,
即x∈(0,+∞)时,f′(x)<0,
∴函数f(x)在(0,+∞)单调递减,此时f(x)<f(0)=0,不符合题意.
③若0<a<1,由g′(x)=4(ax﹣1+a)e2x=0,得x= ![]() ,且x∈(0,
,且x∈(0, ![]() ),g′(x)<0,
),g′(x)<0,
∴函数y=g(x)在(0, ![]() )单调递减.
)单调递减.
∴x∈(0, ![]() )时,g(x)<g(0)=a﹣1<0,即x
)时,g(x)<g(0)=a﹣1<0,即x ![]() 时,f′(x)<0,
时,f′(x)<0,
∴函数y=f(x)在(0, ![]() )单调递减,
)单调递减,
∴x∈(0, ![]() )时,f(x)<f(0)=0,不符合题意.
)时,f(x)<f(0)=0,不符合题意.
综上所述,实数a的取值范围是[1,+∞).
【解析】(1)a=0时,f′(x)=﹣2e2x+1,由此利用导数性质能求出函数f(x)的单调区间.(2)f′(x)=(2ax﹣2+a)e2x+1,令g(x)=(2ax﹣2+a)e2x+1,则g′(x)=4(ax﹣1+a)e2x,由此利用分类讨论思想,结合导数应用能求出实数a的取值范围.
【考点精析】认真审题,首先需要了解利用导数研究函数的单调性(一般的,函数的单调性与其导数的正负有如下关系: 在某个区间![]() 内,(1)如果
内,(1)如果![]() ,那么函数
,那么函数![]() 在这个区间单调递增;(2)如果
在这个区间单调递增;(2)如果![]() ,那么函数
,那么函数![]() 在这个区间单调递减),还要掌握函数的最大(小)值与导数(求函数
在这个区间单调递减),还要掌握函数的最大(小)值与导数(求函数![]() 在
在![]() 上的最大值与最小值的步骤:(1)求函数
上的最大值与最小值的步骤:(1)求函数![]() 在
在![]() 内的极值;(2)将函数
内的极值;(2)将函数![]() 的各极值与端点处的函数值
的各极值与端点处的函数值![]() ,
,![]() 比较,其中最大的是一个最大值,最小的是最小值)的相关知识才是答题的关键.
比较,其中最大的是一个最大值,最小的是最小值)的相关知识才是答题的关键.


科目:高中数学 来源: 题型:
【题目】已知两个集合A,B,满足BA.若对任意的x∈A,存在ai , aj∈B(i≠j),使得x=λ1ai+λ2aj(λ1 , λ2∈{﹣1,0,1}),则称B为A的一个基集.若A={1,2,3,4,5,6,7,8,9,10},则其基集B元素个数的最小值是 .
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某高校调查了200名学生每周的自习时间(单位:小时),制成了如图所示的频率分布直方图,其中自习时间的范围是[17.5,30],样本数据分组为[17.5,20),[20,22.5),[22.5,25),[25,27.5),[27.5,30].根据直方图,若这200名学生中每周的自习时间不超过m小时的人数为164,则m的值约为( ) 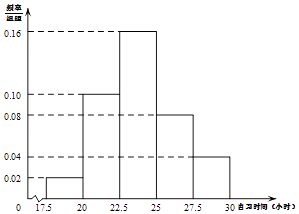
A.26.25
B.26.5
C.26.75
D.27
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图所示的多面体是由一个直平行六面体被平面AEFG所截后得到的,其中∠BAE=∠GAD=45°,AB=2AD=2,∠BAD=60°. 
(1)求证:BD⊥平面ADG;
(2)求此多面体的全面积.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某社区新建了一个休闲小公园,几条小径将公园分成5块区域,如图,社区准备从4种颜色不同的花卉中选择若干种种植在各块区域,要求每个区域随机用一种颜色的花卉,且相邻区域(用公共边的)所选花卉颜色不能相同,则不同种植方法的种数共有( ) 
A.96
B.114
C.168
D.240
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】现有10支队伍参加篮球比赛,规定:比赛采取单循环比赛制,即每支队伍与其他9支队伍各比赛一场;每场比赛中,胜方得2分,负方得0分,平局双方各得1分.下面关于这10支队伍得分的叙述正确的是( )
A.可能有两支队伍得分都是18分
B.各支队伍得分总和为180分
C.各支队伍中最高得分不少于10分
D.得偶数分的队伍必有偶数个
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知f(x)=ln(ax+b)+x2(a≠0).
(1)若曲线y=f(x)在点(1,f(1))处的切线方程为y=x,求a,b的值;
(2)若f(x)≤x2+x恒成立,求ab的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】宿州市某登山爱好者为了解山高y(百米)与气温x(℃)之间的关系,随机统计了4次山高与相应的气温,并制作了对照表,由表中数据,得到线性回归方程为y=﹣2x+a,由此估计山高为72(百米)处的气温为( )
气温x(℃) | 18 | 13 | 10 | ﹣1 |
山高y(百米) | 24 | 34 | 38 | 64 |
A.﹣10
B.﹣8
C.﹣6
D.﹣4
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com