
【题目】已知函数![]()
![]() .
.
(1)若![]() ,求
,求![]() 的单调区间;
的单调区间;
(2)讨论![]() 的零点个数.
的零点个数.
科目:高中数学 来源: 题型:
【题目】团购已成为时下商家和顾客均非常青睐的一种省钱、高校的消费方式,不少商家同时加入多家团购网.现恰有三个团购网站在![]() 市开展了团购业务,
市开展了团购业务, ![]() 市某调查公司为调查这三家团购网站在本市的开展情况,从本市已加入了团购网站的商家中随机地抽取了50家进行调查,他们加入这三家团购网站的情况如下图所示.
市某调查公司为调查这三家团购网站在本市的开展情况,从本市已加入了团购网站的商家中随机地抽取了50家进行调查,他们加入这三家团购网站的情况如下图所示.
(1)从所调查的50家商家中任选两家,求他们加入团购网站的数量不相等的概率;
(2)从所调查的50家商家中任取两家,用![]() 表示这两家商家参加的团购网站数量之差的绝对值,求随机变量
表示这两家商家参加的团购网站数量之差的绝对值,求随机变量![]() 的分布列和数学期望;
的分布列和数学期望;
(3)将频率视为概率,现从![]() 市随机抽取3家已加入团购网站的商家,记其中恰好加入了两个团购网站的商家数为
市随机抽取3家已加入团购网站的商家,记其中恰好加入了两个团购网站的商家数为![]() ,试求事件“
,试求事件“![]() ”的概率.
”的概率.

查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】一旅游区有两个新建项目![]() 、
、![]() .
.![]() 项目的一期投资额
项目的一期投资额![]() 与利润
与利润![]() 近似满足
近似满足![]() .
.![]() 项目的一期投资额
项目的一期投资额![]() 与利润
与利润![]() 的关系如散点图所示,其中
的关系如散点图所示,其中![]()
![]() ,
,![]() ,
,![]() .一商家欲向这两个项目一期随机投资,其中投资
.一商家欲向这两个项目一期随机投资,其中投资![]() 项目不超过10(本题未注明金额单位的,单位均为百万元).投资
项目不超过10(本题未注明金额单位的,单位均为百万元).投资![]() 、
、![]() 相互独立.
相互独立.
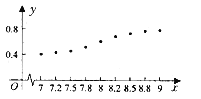
(1)用最小二乘法求![]() 与
与![]() 的回归直线方程;
的回归直线方程;
(2)商家投资![]() 项目的概率是0.4,投资
项目的概率是0.4,投资![]() 项目的概率是0.6.设商家这次投资获得的利润最大值为
项目的概率是0.6.设商家这次投资获得的利润最大值为![]() ,利用(1)的结果,求
,利用(1)的结果,求![]() .
.
附参考公式: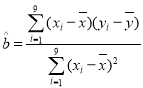 ,
,![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某企业响应省政府号召,对现有设备进行改造,为了分析设备改造前后的效果,现从设备改造前后生产的大量产品中各抽取了![]() 件产品作为样本,检测一项质量指标值,若该项质量指标值落在
件产品作为样本,检测一项质量指标值,若该项质量指标值落在![]() 内的产品视为合格品,否则为不合格品.如图是设备改造前的样本的频率分布直方图,表
内的产品视为合格品,否则为不合格品.如图是设备改造前的样本的频率分布直方图,表![]() 是设备改造后的样本的频数分布表.
是设备改造后的样本的频数分布表.
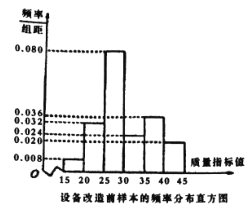
表:设备改造后样本的频数分布表
质量指标值 |
|
|
|
|
|
|
频数 |
|
|
|
|
|
|
(1)完成下面的![]() 列联表,并判断是否有
列联表,并判断是否有![]() 的把握认为该企业生产的这种产品的质量指标值与设备改造有关;
的把握认为该企业生产的这种产品的质量指标值与设备改造有关;
设备改造前 | 设备改造后 | 合计 | |
合格品 | |||
不合格品 | |||
合计 |
(2)根据频率分布直方图和表 提供的数据,试从产品合格率的角度对改造前后设备的优劣进行比较;
(3)企业将不合格品全部销毁后,根据客户需求对合格品进行登记细分,质量指标值落在![]() 内的定为一等品,每件售价
内的定为一等品,每件售价![]() 元;质量指标值落在
元;质量指标值落在![]() 或
或![]() 内的定为二等品,每件售价
内的定为二等品,每件售价![]() 元;其它的合格品定为三等品,每件售价
元;其它的合格品定为三等品,每件售价![]() 元.根据表
元.根据表![]() 的数据,用该组样本中一等品、二等品、三等品各自在合格品中的频率代替从所有产品中抽到一件相应等级产品的概率.现有一名顾客随机购买两件产品,设其支付的费用为
的数据,用该组样本中一等品、二等品、三等品各自在合格品中的频率代替从所有产品中抽到一件相应等级产品的概率.现有一名顾客随机购买两件产品,设其支付的费用为![]() (单位:元),求
(单位:元),求![]() 的分布列和数学期望.
的分布列和数学期望.
附:
|
|
|
|
|
|
|
|
|
|
|
|
![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】本小题满分13分)
工作人员需进入核电站完成某项具有高辐射危险的任务,每次只派一个人进去,且每个人只派一次,工作时间不超过10分钟,如果有一个人10分钟内不能完成任务则撤出,再派下一个人.现在一共只有甲、乙、丙三个人可派,他们各自能完成任务的概率分别![]()
![]() ,假设
,假设![]() 互不相等,且假定各人能否完成任务的事件相互独立.
互不相等,且假定各人能否完成任务的事件相互独立.
(1)如果按甲在先,乙次之,丙最后的顺序派人,求任务能被完成的概率.若改变三个人被派出的先后顺序,任务能被完成的概率是否发生变化?
(2)若按某指定顺序派人,这三个人各自能完成任务的概率依次为![]() ,其中
,其中![]() 是
是![]() 的一个排列,求所需派出人员数目
的一个排列,求所需派出人员数目![]() 的分布列和均值(数字期望)
的分布列和均值(数字期望)![]() ;
;
(3)假定![]() ,试分析以怎样的先后顺序派出人员,可使所需派出的人员数目的均值(数字期望)达到最小.
,试分析以怎样的先后顺序派出人员,可使所需派出的人员数目的均值(数字期望)达到最小.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】每年9月第三周是国家网络安全宣传周.某学校为调查本校学生对网络安全知识的了解情况,组织了《网络信息辨析测试》活动,并随机抽取50人的测试成绩绘制了频率分布直方图如图所示:

(1)某学生的测试成绩是75分,你觉得该同学的测试成绩低不低?说明理由;
(2)将成绩在![]() 内定义为“合格”;成绩在
内定义为“合格”;成绩在![]() 内定义为“不合格”.①请将下面的
内定义为“不合格”.①请将下面的![]() 列联表补充完整; ②是否有90%的把认为网络安全知识的掌握情况与性别有关?说明你的理由;
列联表补充完整; ②是否有90%的把认为网络安全知识的掌握情况与性别有关?说明你的理由;
合格 | 不合格 | 合计 | |
男生 | 26 | ||
女生 | 6 | ||
合计 |
(3)在(2)的前提下,对50人按是否合格,利用分层抽样的方法抽取5人,再从5人中随机抽取2人,求恰好2人都合格的概率.附:
| 0.100 | 0.050 | 0.010 | 0.001 |
| 2.706 | 3.841 | 6.65 | 10.828 |
![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】为了调查“双11”消费活动情况,某校统计小组分别走访了![]() 、
、![]() 两个小区各20户家庭,他们当日的消费额按
两个小区各20户家庭,他们当日的消费额按![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() 分组,分别用频率分布直方图与茎叶图统计如下(单位:元):
分组,分别用频率分布直方图与茎叶图统计如下(单位:元):
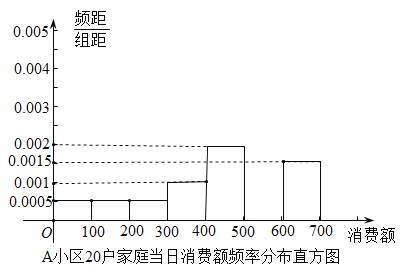
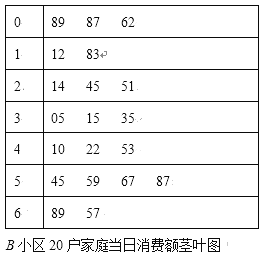
(1)分别计算两个小区这20户家庭当日消费额在![]() 的频率,并补全频率分布直方图;
的频率,并补全频率分布直方图;
(2)分别从两个小区随机选取1户家庭,求这两户家庭当日消费额在![]() 的户数为1时的概率(频率当作概率使用);
的户数为1时的概率(频率当作概率使用);
(3)运用所学统计知识分析比较两个小区的当日网购消费水平.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com