
【题目】已知二次函数f(x)=ax2+(2b﹣1)x+6b﹣a为偶函数,且f(x+1)﹣f(x)=2x+1.
(1)求函数f(x)的解析式;
(2)设g(x)=f(x)+λx,求函数g(x)在[0,1]内的最小值.
【答案】
(1)解:∵二次函数f(x)=ax2+(2b﹣1)x+6b﹣a为偶函数,
∴2b﹣1=0,∴b= ![]() ,
,
∴f(x)=ax2+3﹣a
∵f(x+1)﹣f(x)=2x+1,
∴a(x+1)2+3﹣a﹣(ax2+3﹣a)=2x+1,
∴a=1,
∴f(x)=x2+2;
(2)解:由(1)得g(x)=x2+λx+2,对称轴x=﹣ ![]()
①当﹣ ![]() <0即λ<0时,函数g(x)在[0,1]内的最小值为g(0)=2
<0即λ<0时,函数g(x)在[0,1]内的最小值为g(0)=2
②当0≤ ![]() ≤1,即0≤λ≤2时,函数g(x)在[0,1]内的最小值为g(﹣
≤1,即0≤λ≤2时,函数g(x)在[0,1]内的最小值为g(﹣ ![]() )=2﹣
)=2﹣ ![]()
③当 ![]() >1即λ>2时,函数g(x)在[0,1]内的最小值为g(1)=3+λ.
>1即λ>2时,函数g(x)在[0,1]内的最小值为g(1)=3+λ.
综上所述,函数g(x)在[0,1]内的最小值为 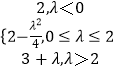
【解析】(1)利用二次函数f(x)=ax2+(2b﹣1)x+6b﹣a为偶函数,求出b,利用f(x+1)﹣f(x)=2x+1,求出a,即可求函数f(x)的解析式;(2)由(1)得g(x)=x2+λx+2,对称轴x=﹣ ![]() ,分类讨论求函数g(x)在[0,1]内的最小值.
,分类讨论求函数g(x)在[0,1]内的最小值.
【考点精析】解答此题的关键在于理解二次函数的性质的相关知识,掌握当![]() 时,抛物线开口向上,函数在
时,抛物线开口向上,函数在![]() 上递减,在
上递减,在![]() 上递增;当
上递增;当![]() 时,抛物线开口向下,函数在
时,抛物线开口向下,函数在![]() 上递增,在
上递增,在![]() 上递减.
上递减.


 99加1领先期末特训卷系列答案
99加1领先期末特训卷系列答案 百强名校期末冲刺100分系列答案
百强名校期末冲刺100分系列答案 好成绩1加1期末冲刺100分系列答案
好成绩1加1期末冲刺100分系列答案 金状元绩优好卷系列答案
金状元绩优好卷系列答案科目:高中数学 来源: 题型:
【题目】机器人![]() (阿法狗)在下围棋时,令人称道的算法策略是:每一手棋都能保证在接下来的十几步后,局面依然是满意的.这种策略给了我们启示:每一步相对完美的决策,对最后的胜利都会产生积极的影响.
(阿法狗)在下围棋时,令人称道的算法策略是:每一手棋都能保证在接下来的十几步后,局面依然是满意的.这种策略给了我们启示:每一步相对完美的决策,对最后的胜利都会产生积极的影响.
下面的算法是寻找“![]() ”中“比较大的数
”中“比较大的数![]() ”,现输入正整数“42,61,80,12,79,18,82,57,31,18“,从左到右依次为
”,现输入正整数“42,61,80,12,79,18,82,57,31,18“,从左到右依次为![]() ,其中最大的数记为
,其中最大的数记为![]() ,则
,则![]() ( )
( )
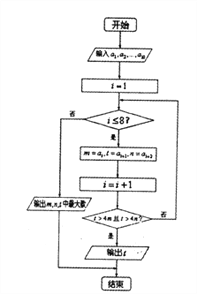
A. 0 B. 1 C. 2 D. 3
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() ,其中常数
,其中常数![]() .
.
(1)若![]() 在
在![]() 上单调递增,求
上单调递增,求![]() 的取值范围;
的取值范围;
(2)令![]() ,将函数
,将函数![]() 的图象向左平移
的图象向左平移![]() 个单位,再向上平移1个单位,得到函数
个单位,再向上平移1个单位,得到函数![]() 的图象.区间
的图象.区间![]() 满足:
满足:![]() 在
在![]() 上至少含有30个零点.在所有满足上述条件的
上至少含有30个零点.在所有满足上述条件的![]() 中,求
中,求![]() 的最小值.
的最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知f(x)为定义在R上的偶函数,当x≥0时,有f(x+3)=﹣f(x),且当x∈[0,3)时,f(x)=log4(x+1),给出下列命题:
①f(2015)>f(2014);
②函数f(x)在定义域上是周期为3的函数;
③直线x﹣3y=0与函数f(x)的图象有2个交点;
④函数f(x)的值域为[0,1).
其中不正确的命题个数是( )
A.1
B.2
C.3
D.4
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在四棱锥P﹣ABCD中,底面ABCD为正方形,平面PAD⊥平面ABCD,点M在线段PB上,PD∥平面MAC,PA=PD= ![]() ,AB=4.
,AB=4. 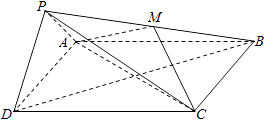
(1)求证:M为PB的中点;
(2)求二面角B﹣PD﹣A的大小;
(3)求直线MC与平面BDP所成角的正弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在直角坐标系xOy中,曲线C的方程为y2=10x,直线l的参数方程为 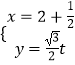 (t为参数),以坐标原点为极点,以x轴的正半轴为极轴建立极坐标系.
(t为参数),以坐标原点为极点,以x轴的正半轴为极轴建立极坐标系.
(1)求曲线C的极坐标方程和直线l的普通方程;
(2)设直线l与曲线C交于A、B两点,求弦长|AB|.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】甲、乙两家商场对同一种商品开展促销活动,对购买该商品的顾客两家商场的奖励方案如下:
甲商场:顾客转动如图所示圆盘,当指针指向阴影部分(图中两个阴影部分均为扇形,且每个扇形圆心角均为![]() ,边界忽略不计)即为中奖·
,边界忽略不计)即为中奖·
乙商场:从装有2个白球、2个蓝球和2个红球的盒子中一次性摸出1球(这些球除颜色外完全相同),它是红球的概率是![]() ,若从盒子中一次性摸出2球,且摸到的是2个相同颜色的球,即为中奖.
,若从盒子中一次性摸出2球,且摸到的是2个相同颜色的球,即为中奖.

(Ⅰ)求实数![]() 的值;
的值;
(Ⅱ)试问:购买该商品的顾客在哪家商场中奖的可能性大?请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知圆![]() 关于直线
关于直线![]() 对称的圆为
对称的圆为![]() .
.
(1)求圆![]() 的方程;
的方程;
(2)过点![]() 作直线
作直线![]() 与圆
与圆![]() 交于
交于![]() 两点,
两点, ![]() 是坐标原点,是否存在这样的直线
是坐标原点,是否存在这样的直线![]() ,使得在平行四边形
,使得在平行四边形![]() 中
中![]() ?若存在,求出所有满足条件的直线
?若存在,求出所有满足条件的直线![]() 的方程;若不存在,请说明理由.
的方程;若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】采用系统抽样方法从960人中抽取32人做问卷调查,为此将他们随即编号为1,2…960,分组后在第一组采用简单随机抽样的方法抽到的号码为5,抽到的32人中,编号落入区间[1,450]的人做问卷A,编号落入区间[451,750]的人做问卷B,其余的人做问卷C,则抽到的32人中,做问卷C的人数为( )
A.15
B.10
C.9
D.7
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com