
【题目】设椭圆![]() :
:![]() 的离心率为
的离心率为![]() ,椭圆
,椭圆![]() 上一点
上一点![]() 到左右两个焦点
到左右两个焦点![]() 、
、![]() 的距离之和是4.
的距离之和是4.
(1)求椭圆的方程;
(2)已知过![]() 的直线与椭圆
的直线与椭圆![]() 交于
交于![]() 、
、![]() 两点,且两点与左右顶点不重合,若
两点,且两点与左右顶点不重合,若![]() ,求四边形
,求四边形![]() 面积的最大值.
面积的最大值.
 全优点练单元计划系列答案
全优点练单元计划系列答案科目:高中数学 来源: 题型:
【题目】已知点![]() ,
,![]() 的两顶点
的两顶点![]() ,且点
,且点![]() 满足
满足![]()
(1)求动点![]() 的轨迹方程;
的轨迹方程;![]()
(2)设![]() ,求动点
,求动点![]() 的轨迹方程;
的轨迹方程;
(3)过点![]() 的动直线
的动直线![]() 与曲线
与曲线![]() 交于不同两点
交于不同两点![]() ,过点
,过点![]() 作
作![]() 轴垂线
轴垂线![]() ,试判断直线
,试判断直线![]() 与直线
与直线![]() 的交点是否恒在一条定直线上?若是,求该定直线的方程,否则,说明理由.
的交点是否恒在一条定直线上?若是,求该定直线的方程,否则,说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某老师是省级课题组的成员,主要研究课堂教学目标达成度,为方便研究,从实验班中随机抽取30次的随堂测试成绩进行数据分析.已知学生甲的30次随堂测试成绩如下(满分为100分):
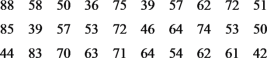
(1)把学生甲的成绩按![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() 分成6组,列出频率分布表,并画出频率分布直方图:
分成6组,列出频率分布表,并画出频率分布直方图:
(2)为更好的分析学生甲存在的问题,从随堂测试成绩50分以下(不包括50分)的试卷中随机抽取3份进行分析,求恰有2份成绩在![]() 内的概率.
内的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图所示四棱锥![]() 的底面为正方形,
的底面为正方形,![]() 平面
平面![]() 则下列结论中不正确的是( )
则下列结论中不正确的是( )

A.![]() B.
B.![]() 平面
平面![]()
C.直线![]() 与平面
与平面![]() 所成的角等于30°D.SA与平面SBD所成的角等于SC与平面SBD所成的角
所成的角等于30°D.SA与平面SBD所成的角等于SC与平面SBD所成的角
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某校高一年级模仿《中国诗词大会》节目举办学校诗词大会,进入正赛的条件为:电脑随机抽取10首古诗,参赛者能够正确背诵6首及以上的进入正赛,若学生甲参赛,他背诵每一首古诗的正确的概率均为![]()
(1)求甲进入正赛的概率;
(2)若进入正赛,则采用积分淘汰制,规则是:电脑随机抽取4首古诗,每首古诗背诵正确加2分,错误减1分.由于难度增加,甲背诵每首古诗正确的概率为![]() ,求甲在正赛中积分
,求甲在正赛中积分![]() 的概率分布列及数学期望.
的概率分布列及数学期望.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如果数列![]() ,
,![]() ,…,
,…,![]() (m ≥ 3,
(m ≥ 3,![]() )满足:①
)满足:①![]() <
<![]() <…<
<…<![]() ;②存在实数
;②存在实数![]() ,
,![]() ,
,![]() ,…,
,…,![]() 和d,使得
和d,使得![]() ≤
≤![]() <
<![]() ≤
≤![]() <
<![]() ≤
≤![]() <…≤
<…≤![]() <
<![]() ,且对任意0 ≤ i ≤ m﹣1(I
,且对任意0 ≤ i ≤ m﹣1(I ![]() ),均有
),均有![]() ,那么称数列
,那么称数列![]() ,
,![]() ,…,
,…,![]() 是“Q数列”.
是“Q数列”.
(1)判断数列1,3,6,10是不是“Q数列”,并说明理由;
(2)已知k,t均为常数,且k>0,求证:对任意给定的不小于3的正整数m,数列![]()
![]() (n=1,2,…,m)都是“Q数列”;
(n=1,2,…,m)都是“Q数列”;
(3)若数列![]() (n=1,2,…,m)是“Q数列”,求m的所有可能值.
(n=1,2,…,m)是“Q数列”,求m的所有可能值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某医院用光电比色计检查尿汞时,得尿汞含量(毫克/升)与消光系数如下表:
尿汞含量 | 2 | 4 | 6 | 8 | 10 |
消光系数 | 64 | 138 | 205 | 285 | 360 |
(1)作散点图;
(2)如果![]() 与
与![]() 之间具有线性相关关系,求回归线直线方程;
之间具有线性相关关系,求回归线直线方程;
(3)估计尿汞含量为9毫克/升时消光系数.
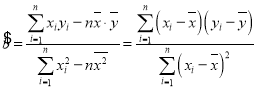 ,
,![]() .
.
参考数据:![]() ,
,![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】(13分)如图,在四棱锥P﹣ABCD中,底面ABCD为平行四边形,∠ADC=45°,AD=AC=1,O为AC中点,PO⊥平面ABCD,PO=2,M为PD中点.

(Ⅰ)证明:PB∥平面ACM;
(Ⅱ)证明:AD⊥平面PAC;
(Ⅲ)求直线AM与平面ABCD所成角的正切值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com