Question

6．已知矩形ABCD中，AB=2，AD=1，M为CD的中点．如图将△ADM沿AM折起，使得平面ADM⊥平面ABCM．
（Ⅰ）求证：BM⊥平面ADM；
（Ⅱ）若点E是线段DB上的中点，求三棱锥E-ABM的体积V₁与四棱锥D-ABCM的体积V₂之比．

Answer 1

分析 （Ⅰ）推导出BM⊥AM，BM⊥AM，由此能证明BM⊥平面ADM．
（Ⅱ）推导出${V_1}=\frac{1}{2}{V_{D-ABM}}$，${S_1}=\frac{2}{3}{S_2}$，且${V_2}=\frac{3}{2}{V_{D-ABM}}$，由此能求出三棱锥E-ABM的体积V₁与四棱锥D-ABCM的体积V₂之比．

解答 （本小题满分12分）
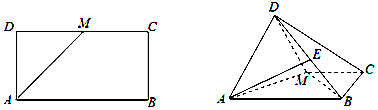
证明：（Ⅰ）因为矩形ABCD中，AB=2，AD=1，M为CD的中点，
所以$AM=BM=\sqrt{2}$，所以AM²+BM²=AB²，所以BM⊥AM．…（3分）
因为平面ADM⊥平面ABCM，平面ADM∩平面ABCM=AM，
又BM?平面ABCM，且BM⊥AM，
∴BM⊥平面ADM．…（6分）
解：（Ⅱ）因为E为DB的中点，所以${V_1}=\frac{1}{2}{V_{D-ABM}}$，…（8分）
又直角三角形ABM的面积${S_1}=\frac{1}{2}•\sqrt{2}•\sqrt{2}=1$，
梯形ABCM的面积${S_2}=\frac{1}{2}•（{1+2}）•1=\frac{3}{2}$，
所以${S_1}=\frac{2}{3}{S_2}$，且${V_2}=\frac{3}{2}{V_{D-ABM}}$，…（11分）
所以$\frac{V_1}{V_2}=\frac{{\frac{1}{2}{V_{D-ABM}}}}{{\frac{3}{2}{V_{D-ABM}}}}=\frac{1}{3}$．…（12分）

点评 本题考查线面垂直的证明，考查两个几何体的体积的比值的求法，是中档题，解题时要认真审题，注意空间思维能力的培养．