（xn+
），n∈N. （Ⅰ）证明：对n≥2，总有xn≥
；
（Ⅱ）证明：对n≥2，总有xn≥xn+1；
（Ⅲ）若数列｛xn｝的极限存在，且大于零，求
xn的值.
（19）本小题主要考查数列、数列极限、不等式等基本知识，考查逻辑能力.
（Ⅰ）证明：由x1=a＞0及xn+1=（xn+），可归纳证明xn＞0（没有证明过程不扣分）.
从而有xn+1=（xn+）≥
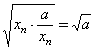（n∈N）,
所以，当n≥2时，xn≥
成立.
（Ⅱ）证法一：当n≥2时，因为xn≥
＞0，xn+1=
（xn+
），
所以xn+1－xn=
（xn+
）－xn =
·
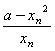≤0，
故当n≥2时，xn≥xn+1成立
证法二：当n≥2时，因为xn≥
＞0，xn+1=
（xn+
），
所以
=
≤
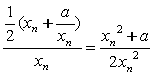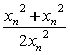=1，
故当n≥2时，xn≥xn+1成立.
（Ⅲ）解：记
xn=A，则
xn+1=A，且A＞0.
由xn+1=
（xn+
），
得
xn+1=
（
xn+
），
即A=
（A+
）.
由A＞0，解得A=
，故
xn=
.
科目：高中数学 来源： 题型：
（xn+
），n∈N. （Ⅰ）证明：对n≥2，总有xn≥
;
（Ⅱ）证明：对n≥2，总有xn≥xn+1.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com