
 、
、 满足|
满足| -
- |=|
|=|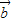 |,则下列结论正确的个数是( )
|,则下列结论正确的个数是( ) 、
、 的夹角恒为锐角;
的夹角恒为锐角; |2>
|2> •
• ;
; |>|
|>| -2
-2 |;
|; |<|2
|<|2 -
- |.
|. 、
、 、
、 -
- 组成的三角形是等腰三角形,判定正误即可;
组成的三角形是等腰三角形,判定正误即可;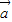 |<|2
|<|2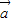 -
-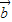 |,得到4|
|,得到4|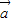 |cos<
|cos<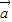 ,
,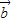 ><|
><|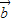 |不一定成立,说明正误即可.
|不一定成立,说明正误即可.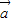 、
、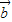 满足|
满足|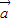 -
-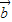 |=|
|=|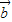 |,所以由向量
|,所以由向量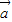 、
、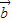 、
、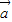 -
-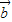 组成的三角形是等腰三角形,
组成的三角形是等腰三角形,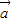 是底边,所以向量
是底边,所以向量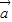 、
、 的夹角恒为锐角,①正确;
的夹角恒为锐角,①正确;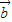 |2>
|2>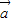 •
•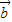 =|
=|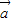 |•|
|•|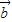 |cos<
|cos<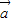 ,
,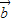 >⇒2|
>⇒2|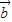 |>|
|>|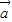 |cos<
|cos<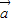 ,
,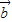 >,
>,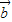 |+|
|+|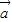 -
-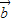 |=2|
|=2|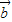 |>|
|>|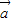 |>|
|>|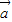 |cos<
|cos<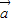 ,
,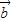 >,所以②正确;
>,所以②正确;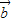 |>|
|>|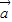 -2
-2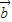 |⇒4|
|⇒4|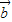 |2>|
|2>|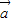 -2
-2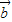 |2=|
|2=|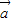 |2-4|
|2-4|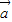 |•|
|•|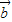 |cos<
|cos<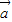 ,
,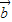 >+4|
>+4|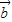 |2
|2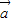 |•|
|•|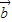 |cos<
|cos<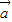 ,
,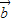 >>|
>>|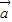 |2⇒4•|
|2⇒4•|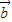 |cos<
|cos<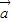 ,
,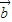 >>|
>>|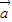 |,
|,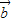 |cos<
|cos<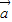 ,
,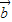 >=|
>=|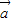 |,所以4|
|,所以4|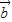 |cos<
|cos<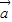 ,
,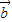 >>|
>>|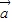 |,③正确;
|,③正确;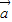 |<|2
|<|2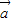 -
-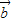 |⇒4|
|⇒4|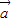 |cos<
|cos<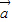 ,
,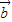 ><|
><|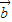 |,而4|
|,而4|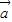 |cos<
|cos< ,
,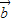 ><|
><|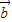 |不一定成立,所以④不正确.
|不一定成立,所以④不正确.

科目:高中数学 来源: 题型:单选题
 、
、 满足|
满足| -
- |=|
|=| |,则下列结论正确的个数是
|,则下列结论正确的个数是 、
、 的夹角恒为锐角;
的夹角恒为锐角; |2>
|2> •
• ;
; |>|
|>| -2
-2 |;
|; |<|2
|<|2 -
- |.
|.查看答案和解析>>
科目:高中数学 来源:2011-2012学年江苏省南京市六合高级中学高三(上)数学寒假作业(4)(解析版) 题型:填空题
 、
、 满足|
满足| -
- |=|
|=| |,则下列结论正确的个数是 .
|,则下列结论正确的个数是 . 、
、 的夹角恒为锐角; ②2|
的夹角恒为锐角; ②2| |2>
|2> •
• ; ③|2
; ③|2 |>|
|>| -2
-2 |; ④|2
|; ④|2 |<|2
|<|2 -
- |.
|.查看答案和解析>>
科目:高中数学 来源:2012年新人教A版高考数学一轮复习单元质量评估04(第四章)(理科)(解析版) 题型:选择题
 、
、 满足|
满足| -
- |=|
|=| |,则下列结论正确的个数是( )
|,则下列结论正确的个数是( ) 、
、 的夹角恒为锐角;
的夹角恒为锐角; |2>
|2> •
• ;
; |>|
|>| -2
-2 |;
|; |<|2
|<|2 -
- |.
|.查看答案和解析>>
科目:高中数学 来源:江苏同步题 题型:填空题
 、
、 满足|
满足| ﹣
﹣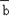 |=|
|=| |,则下列结论正确的个数是( )
|,则下列结论正确的个数是( ) 、
、 的夹角恒为锐角; ②2|
的夹角恒为锐角; ②2| |2>
|2>
 ; ③|2
; ③|2 |>|
|>| ﹣2
﹣2 |; ④|2
|; ④|2 |<|2
|<|2 ﹣
﹣ |.
|.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com