
【题目】记函数f(x)=lg(1﹣ax2)的定义域、值域分别为集合A,B.
(1)当a=1时,求A∩B;
(2)若“x∈A”是“x∈B”的必要不充分条件,求实数a的取值范围.
【答案】
(1)解:当a=1时,f(x)=lg(1﹣x2),由1﹣x2>0,得A=(﹣1,1).
又0<1﹣x2≤1,所以B=(﹣∞,0].
故A∩B=(﹣1,0]
(2)解:“x∈A”是“x∈B”的必要不充分条件BA.
①当a=0时,A=R,B={0},适合题意;
②当a<0时,A=R,B=[0,+∞),适合题意;
③当a>0时, ![]() ,B=(﹣∞,0],不适合题意.
,B=(﹣∞,0],不适合题意.
综上所述,实数a的取值范围是(﹣∞,0]
【解析】(1)首先求出当a=1时,f(x)的定义域,值域,利用交集的定义求出结果。(2)根据题意分情况讨论a的取值,讨论验证得到a的取值范围。
【考点精析】掌握集合的交集运算是解答本题的根本,需要知道交集的性质:(1)A∩B![]() A,A∩B
A,A∩B![]() B,A∩A=A,A∩
B,A∩A=A,A∩![]() =
=![]() ,A∩B=B∩A;(2)若A∩B=A,则A
,A∩B=B∩A;(2)若A∩B=A,则A![]() B,反之也成立.
B,反之也成立.


科目:高中数学 来源: 题型:
【题目】经销商经销某种农产品,在一个销售季度内,每售出1t该产品获利润500元,未售出的产品,每1t亏损300元.根据历史资料,得到销售季度内市场需求量的频率分布直方图,如图所示.经销商为下一个销售季度购进了130t该农产品.以X(单位:t,100≤X≤150)表示下一个销售季度内的市场需求量,T(单位:元)表示下一个销售季度内经销该农产品的利润.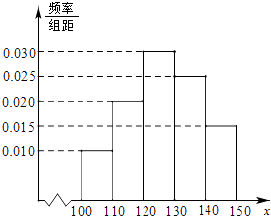
(Ⅰ)将T表示为X的函数;
(Ⅱ)根据直方图估计利润T不少于57000元的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数 ![]() ,且f(1)=1,f(﹣2)=4.
,且f(1)=1,f(﹣2)=4.
(1)求a、b的值;
(2)已知定点A(1,0),设点P(x,y)是函数y=f(x)(x<﹣1)图象上的任意一点,求|AP|的最小值,并求此时点P的坐标;
(3)当x∈[1,2]时,不等式 ![]() 恒成立,求实数m的取值范围.
恒成立,求实数m的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数 ![]()
(1)判断函数f(x)的奇偶性,并说明理由;
(2)证明:f(x)在(﹣1,+∞)上为增函数;
(3)证明:方程f(x)=0没有负数根.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知在等差数列{an}中,Sn为其前n项和,a2=2,S5=15;等比数列{bn}的前n项和 ![]() .
.
( I)求数列{an},{bn}的通项公式;
( II)设cn=anbn , 求数列{cn}的前n项和Cn .
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在平面直角坐标系xOy中,椭圆E: ![]() =1(a>b>0)的左顶点为A(﹣2,0),离心率为
=1(a>b>0)的左顶点为A(﹣2,0),离心率为 ![]() ,过点A的直线l与椭圆E交于另一点B,点C为y轴上的一点.
,过点A的直线l与椭圆E交于另一点B,点C为y轴上的一点.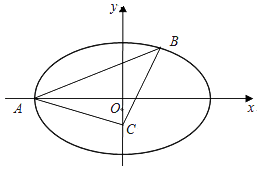
(1)求椭圆E的标准方程;
(2)若△ABC是以点C为直角顶点的等腰直角三角形,求直线l的方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=(a2﹣3a+3)ax是指数函数,
(1)求f(x)的表达式;
(2)判断F(x)=f(x)﹣f(﹣x)的奇偶性,并加以证明
(3)解不等式:loga(1﹣x)>loga(x+2)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】解答题
(Ⅰ)已知 ![]() ,其中ai∈R,i=1,2,…10.
,其中ai∈R,i=1,2,…10.
(i)求a0+a1+a2+…+a10;
(ii)求a7 .
(Ⅱ)2017年5月,北京召开“一带一路”国际合作高峰论坛.组委会将甲、乙、丙、丁、戊五名志愿者分配到翻译、导游、礼仪、司机四个不同的岗位,每个岗位至少有一人参加,且五人均能胜任这四个岗位.
(i)若每人不准兼职,则不同的分配方案有几种?
(ii)若甲乙被抽调去别的地方,剩下三人要求每人必兼两职,则不同的分配方案有几种?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com