
【题目】已知数列{an}是首项 ![]() ,公比
,公比 ![]() 的等比数列.设
的等比数列.设 ![]() (n∈N*). (Ⅰ)求证:数列{bn}为等差数列;
(n∈N*). (Ⅰ)求证:数列{bn}为等差数列;
(Ⅱ)设cn=an+b2n , 求数列{cn}的前n项和Tn .
【答案】解:(Ⅰ)证明:∵数列{an}是首项 ![]() ,公比
,公比 ![]() 的等比数列, ∴
的等比数列, ∴ ![]() ,则
,则 ![]() =
= ![]() .
.
∴bn+1﹣bn=[2(n+1)﹣1]﹣(2n﹣1)=2.
则数列{bn}是以2为公差的等差数列;
(Ⅱ)解:cn=an+b2n= ![]() .
.
∴数列{cn}的前n项和Tn=c1+c2+…+cn=[ ![]() ]+4(1+2+…+n)﹣n
]+4(1+2+…+n)﹣n
= 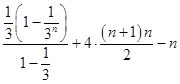 =
= ![]() =
= ![]() .
.
【解析】(Ⅰ)由已知求出等比数列的通项公式,代入 ![]() 可得数列{bn}的通项公式,由等差数列的定义证明数列{bn}为等差数列;(Ⅱ)把数列{an}、{bn}的通项公式代入cn=an+b2n , 分组后再由等差数列与等比数列的前n项和求数列{cn}的前n项和Tn .
可得数列{bn}的通项公式,由等差数列的定义证明数列{bn}为等差数列;(Ⅱ)把数列{an}、{bn}的通项公式代入cn=an+b2n , 分组后再由等差数列与等比数列的前n项和求数列{cn}的前n项和Tn .
【考点精析】本题主要考查了数列的前n项和和数列的通项公式的相关知识点,需要掌握数列{an}的前n项和sn与通项an的关系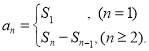 ;如果数列an的第n项与n之间的关系可以用一个公式表示,那么这个公式就叫这个数列的通项公式才能正确解答此题.
;如果数列an的第n项与n之间的关系可以用一个公式表示,那么这个公式就叫这个数列的通项公式才能正确解答此题.


 开心蛙状元测试卷系列答案
开心蛙状元测试卷系列答案科目:高中数学 来源: 题型:
【题目】已知函数f(x)=x﹣alnx(a∈R)
(1)当a=2时,求曲线y=f(x)在点A(1,f(1))处的切线方程;
(2)求函数f(x)的极值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知等差数列{an}的前n项和为Sn , 且a1=10,S5≥S6 , 下列四个命题中,假命题是( )
A.公差d的最大值为﹣2
B.S7<0
C.记Sn的最大值为K,K的最大值为30
D.a2016>a2017
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=ex﹣alnx﹣a. (Ⅰ)当a=e时,求曲线y=f(x)在点(1,f(1))处的切线方程;
(Ⅱ)证明:对于a∈(0,e),f(x)在区间 ![]() 上有极小值,且极小值大于0.
上有极小值,且极小值大于0.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】函数f(x)=x2﹣bx+c满足f(1+x)=f(1﹣x)且f(0)=3,则f(bx)和f(cx)的大小关系是( )
A.f(bx)≤f(cx)
B.f(bx)≥f(cx)
C.f(bx)>f(cx)
D.大小关系随x的不同而不同
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】四棱锥P﹣ABCD中,PD⊥面ABCD,底面ABCD是菱形,且PD=DA=2,∠CDA=60°,过点B作直线l∥PD,Q为直线l上一动点. 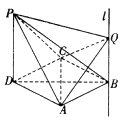
(1)求证:QP⊥AC;
(2)当二面角Q﹣AC﹣P的大小为120°时,求QB的长;
(3)在(2)的条件下,求三棱锥Q﹣ACP的体积.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知向量 ![]() =(sinx,mcosx),
=(sinx,mcosx), ![]() =(3,﹣1).
=(3,﹣1).
(1)若 ![]() ∥
∥ ![]() ,且m=1,求2sin2x﹣3cos2x的值;
,且m=1,求2sin2x﹣3cos2x的值;
(2)若函数f(x)= ![]()
![]() 的图象关于直线x=
的图象关于直线x= ![]() 对称,求函数f(2x)在[
对称,求函数f(2x)在[ ![]() ,
, ![]() ]上的值域.
]上的值域.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com