
【题目】为了治理大气污染,某市2017年初采用了一系列措施,比如“煤改电”,“煤改气”,“整治散落污染企业”等.下表是该市2016年11月份和2017年11月份的空气质量指数(![]() )(
)(![]() 指数越小,空气质量越好)统计表.根据表中数据回答下列问题:
指数越小,空气质量越好)统计表.根据表中数据回答下列问题:
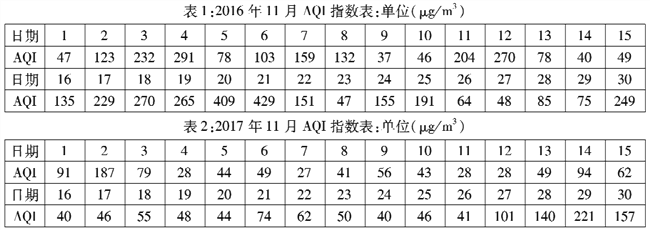
(1)将2017年11月的空气质量指数![]() 数据用该天的对应日期作为样本编号,再用系统抽样方法从中抽取6个
数据用该天的对应日期作为样本编号,再用系统抽样方法从中抽取6个![]() 数据,若在2017年11月16日到11月20日这五天中用简单随机抽样抽取到的样本的编号是19号,写出抽出的样本数据;
数据,若在2017年11月16日到11月20日这五天中用简单随机抽样抽取到的样本的编号是19号,写出抽出的样本数据;
(2)从(1)中抽出的6个样本数据中随机抽取2个,求这2个![]() 数据之差的绝对值小于30的概率;
数据之差的绝对值小于30的概率;
(3)根据《环境空气质量指数(![]() )技术规定(试行)》规定:当空气质量指数为
)技术规定(试行)》规定:当空气质量指数为![]() (含50)时,空气质量级别为一级,求出这两年11月空气质量指数为一级的概率,你认为该市2017年初开始采取的这些大气污染治理措施是否有效?
(含50)时,空气质量级别为一级,求出这两年11月空气质量指数为一级的概率,你认为该市2017年初开始采取的这些大气污染治理措施是否有效?
【答案】(1)见解析;(2)![]() .(3)见解析.
.(3)见解析.
【解析】试题分析:(1)利用系统抽样的方法,即可得到抽出的样本数据;
(2)从(1)中抽出的![]() 个样本数据中随机抽出
个样本数据中随机抽出![]() 个,基本事件总数,再利用古典概型的概率计算公式,即可求解相应的概率;
个,基本事件总数,再利用古典概型的概率计算公式,即可求解相应的概率;
(3)分别求得![]() 年
年![]() 月和
月和![]() 年
年![]() 月
月![]() 指数为一级的概率,比较即可得到结论.
指数为一级的概率,比较即可得到结论.
试题解析:
(1)系统抽样,分段间隔![]() ,
,
这些抽出的样本的编号依次是4号、9号、14号、19号、24号、29号,
对应的样本数据依次是![]() 、56、94、48、40、221.
、56、94、48、40、221.
(2)从(1)中抽出的6个样本数据中随机抽出2个,基本事件总数为![]() ,
,
这两个![]() 数据之差的绝对值小于30的有6组:
数据之差的绝对值小于30的有6组:
![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,
所以这2个![]() 数据之差的绝对值小于概率
数据之差的绝对值小于概率![]() .
.
(3)2016年11月![]() 指数为一级的概率
指数为一级的概率![]() ,
,
2017年11月![]() 指数为一级的概率
指数为一级的概率![]() ,
,
![]() ,说明这些措施是有效的.
,说明这些措施是有效的.


 名师点拨卷系列答案
名师点拨卷系列答案 英才计划期末调研系列答案
英才计划期末调研系列答案科目:高中数学 来源: 题型:
【题目】设函数f(x)=ax2-a-lnx,其中a ∈R.
(I)讨论f(x)的单调性;
(II)确定a的所有可能取值,使得![]() 在区间(1,+∞)内恒成立(e=2.718…为自然对数的底数)。
在区间(1,+∞)内恒成立(e=2.718…为自然对数的底数)。
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设函数f(x)的定义域为(-3,3),
满足f(-x)=-f(x),且对任意x,y,都有f(x)-f(y)=f(x-y),当x<0时,f(x)>0,f(1)=-2.
(1)求f(2)的值;
(2)判断f(x)的单调性,并证明;
(3)若函数g(x)=f(x-1)+f(3-2x),求不等式g(x)≤0的解集.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某综艺节目为比较甲、乙两名选手的各项能力(指标值满分为5分,分值高者为优),绘制了如图所示的六维能力雷达图,图中点A表示甲的创造力指标值为4,点B表示乙的空间能力指标值为3,则下面叙述正确的是

A. 乙的记忆能力优于甲的记忆能力
B. 乙的创造力优于观察能力
C. 甲的六大能力整体水平优于乙
D. 甲的六大能力中记忆能力最差
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知![]() 、
、![]() 分别是离心率为
分别是离心率为![]() 的椭圆
的椭圆![]() :
:![]() 的左、右焦点,点
的左、右焦点,点![]() 是椭圆
是椭圆![]() 上异于其左、右顶点的任意一点,过右焦点
上异于其左、右顶点的任意一点,过右焦点![]() 作
作![]() 的外角平分线
的外角平分线![]() 的垂线
的垂线![]() ,交
,交![]() 于点
于点![]() ,且
,且![]() (
(![]() 为坐标原点).
为坐标原点).
(1)求椭圆![]() 的方程;
的方程;
(2)若点![]() 在圆
在圆![]() 上,且在第一象限,过
上,且在第一象限,过![]() 作圆
作圆![]() 的切线交椭圆于
的切线交椭圆于![]() 、
、![]() 两点,问:
两点,问:![]() 的周长是否为定值?如果是,求出该定值;如果不是,说明理由.
的周长是否为定值?如果是,求出该定值;如果不是,说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设![]() 或
或![]() ,
,![]() ,若
,若![]() 是
是![]() 的充分条件.
的充分条件.
(1)求证:函数![]() 的图像总在直线
的图像总在直线![]() 的下方;
的下方;
(2)是否存在实数![]() ,使得不等式
,使得不等式![]() 对一切实数
对一切实数![]() 恒成立?若存在,求出
恒成立?若存在,求出![]() 的取值范围;若不存在,说明理由.
的取值范围;若不存在,说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com