
【题目】如图,三棱柱![]() 中,侧面
中,侧面![]() 为菱形,
为菱形,![]() .
.

(1)证明:![]() ;
;
(2)若![]() ,
,![]() ,
,![]() ,求二面角
,求二面角![]() 的余弦值.
的余弦值.
科目:高中数学 来源: 题型:
【题目】△ABC的角A、B、C的对边分别为a、b、c,![]() =(2b-c,a),
=(2b-c,a),![]() =(cosA,-cosC),且
=(cosA,-cosC),且![]() ⊥
⊥![]() .
.
(Ⅰ)求角A的大小;
(Ⅱ)当y=2sin2B+sin(2B+![]() )取最大值时,求角
)取最大值时,求角![]() 的大小.
的大小.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设经过点![]() 的直线
的直线![]() 与抛物线
与抛物线![]() 相交于
相交于![]() 、
、![]() 两点,经过点
两点,经过点![]() 的直线
的直线![]() 与抛物线
与抛物线![]() 相切于点
相切于点![]() .
.
(1)当![]() 时,求
时,求![]() 的取值范围;
的取值范围;
(2)问是否存在直线![]() ,
,![]() 使得
使得![]() 成立,若存在,求出
成立,若存在,求出![]() 的取值范围;若不存在,请说明理由.
的取值范围;若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在三棱锥P-ABC中,已知![]() ,顶点P在平面ABC上的射影为
,顶点P在平面ABC上的射影为![]() 的外接圆圆心.
的外接圆圆心.
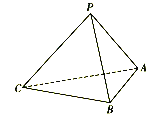
(1)证明:平面![]() 平面ABC;
平面ABC;
(2)若点M在棱PA上,![]() ,且二面角P-BC-M的余弦值为
,且二面角P-BC-M的余弦值为![]() ,试求
,试求![]() 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,A、B为椭圆C:![]() 短轴的上、下顶点,P为直线l:y=2上一动点,连接PA并延长交椭圆于点M,连接PB交椭圆于点N,已知直线MA,MB的斜率之积恒为
短轴的上、下顶点,P为直线l:y=2上一动点,连接PA并延长交椭圆于点M,连接PB交椭圆于点N,已知直线MA,MB的斜率之积恒为![]() .
.

(1)求椭圆C的标准方程;
(2)若直线MN与x轴平行,求直线MN的方程;
(3)求四边形AMBN面积的最大值,并求对应的点P的坐标.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某印刷厂为了研究单册书籍的成本![]() (单位:元)与印刷册数
(单位:元)与印刷册数![]() (单位:千册)之间的关系,在印制某种书籍时进行了统计,相关数据见下表:
(单位:千册)之间的关系,在印制某种书籍时进行了统计,相关数据见下表:
印刷册数 |
|
|
|
|
|
单册成本 |
|
|
|
|
|
根据以上数据,技术人员分别借助甲、乙两种不同的回归模型,得到两个回归方程,方程甲:![]() ,方程乙:
,方程乙:![]() .
.
(1)为了评价两种模型的拟合效果,完成以下任务.
①完成下表(计算结果精确到![]() );
);
印刷册数 |
|
|
|
|
| |
单册成本 |
|
|
|
|
| |
模型甲 | 估计值 |
|
|
| ||
残差 |
|
|
| |||
模型乙 | 估计值 |
|
|
| ||
残差 |
|
|
| |||
②分别计算模型甲与模型乙的残差平方和,并通过比较,判断哪个模型拟合效果更好.
(2)该书上市之后,受到广大读者热烈欢迎,不久便全部售罄,于是印刷厂决定进行二次印刷,根据市场调查,新需求量为![]() 千册,若印刷厂以每册
千册,若印刷厂以每册![]() 元的价格将书籍出售给订货商,求印刷厂二次印刷
元的价格将书籍出售给订货商,求印刷厂二次印刷![]() 千册获得的利润?(按(1)中拟合效果较好的模型计算印刷单册书的成本).
千册获得的利润?(按(1)中拟合效果较好的模型计算印刷单册书的成本).
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】中国改革开放以来经济发展迅猛,某一线城市的城镇居民2012~2018年人均可支配月收入散点图如下(年份均用末位数字减1表示).
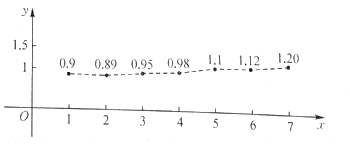
(1)由散点图可知,人均可支配月收入y(万元)与年份x之间具有较强的线性相关关系,试求y关于x的回归方程(系数精确到0.001),依此相关关系预测2019年该城市人均可支配月收入;
(2)在2014~2018年的五个年份中随机抽取两个数据作样本分析,求所取的两个数据中,人均可支配月收入恰好有一个超过1万元的概率.
注: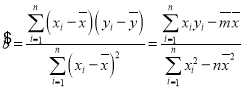 ,
,![]() ,
,![]() ,
,![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com