
【题目】设A,B是R中两个子集,对于x∈R,定义:![]() ,
,
①若AB.则对任意x∈R,m(1-n)=______;
②若对任意x∈R,m+n=1,则A,B的关系为______.
 全优点练单元计划系列答案
全优点练单元计划系列答案科目:高中数学 来源: 题型:
【题目】为了解共享单车在![]() 市的使用情况,某调查机构借助网络进行了问卷调查,并从参与调查的网友中随机抽取了
市的使用情况,某调查机构借助网络进行了问卷调查,并从参与调查的网友中随机抽取了![]() 人进行分析,得到如下列联表(单位:人).
人进行分析,得到如下列联表(单位:人).
经常使用 | 偶尔使用或不使用 | 合计 | |
|
|
|
|
|
|
|
|
合计 |
|
|
|
(1)根据以上数据,能否在犯错误的概率不超过![]() 的前提下认为
的前提下认为![]() 市使用共享单车的情况与年龄有关;
市使用共享单车的情况与年龄有关;
(2)(i)现从所选取的![]() 岁以上的网友中,采用分层抽样的方法选取
岁以上的网友中,采用分层抽样的方法选取![]() 人,再从这
人,再从这![]() 人中随机选出
人中随机选出![]() 人赠送优惠券,求选出的
人赠送优惠券,求选出的![]() 人中至少有
人中至少有![]() 人经常使用共享单车的概率;
人经常使用共享单车的概率;
(ii)将频率视为概率,从![]() 市所有参与调查的网友中随机选取
市所有参与调查的网友中随机选取![]() 人赠送礼品,记其中经常使用共享单车的人数为
人赠送礼品,记其中经常使用共享单车的人数为![]() ,求
,求![]() 的数学期望和方差.
的数学期望和方差.
参考公式: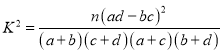 ,其中
,其中![]() .
.
参考数据:
|
|
|
|
|
|
|
|
|
|
|
|
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知抛物线![]() ,斜率为
,斜率为![]() 的直线
的直线![]() 交抛物线
交抛物线![]() 于
于![]() ,
,![]() 两点,当直线
两点,当直线![]() 过点
过点![]() 时,以
时,以![]() 为直径的圆与直线
为直径的圆与直线![]() 相切.
相切.
(1)求抛物线![]() 的方程;
的方程;
(2)与![]() 平行的直线
平行的直线![]() 交抛物线于
交抛物线于![]() ,
,![]() 两点,若平行线
两点,若平行线![]() ,
,![]() 之间的距离为
之间的距离为![]() ,且
,且![]() 的面积是
的面积是![]() 面积的
面积的![]() 倍,求
倍,求![]() 和
和![]() 的方程.
的方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某人在塔的正东方向沿着南偏西60°的方向前进40 m以后,望见塔在东北方向上,若沿途测得塔的最大仰角为30°,则塔高为________________m.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】对任意![]() ,
,![]() ,
,![]() ,给出下列命题:
,给出下列命题:
①“![]() ”是“
”是“![]() ”的充要条件;
”的充要条件;
②“![]() 是无理数”是“
是无理数”是“![]() 是无理数”的充要条件;
是无理数”的充要条件;
③“![]() ”是“
”是“![]() ”的必要条件,
”的必要条件,
④“![]() ”是“
”是“![]() ”的充分条件.
”的充分条件.
其中真命题的个数为().
A.1个
B.2个
C.3个
D.4个
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com