
【题目】如图,在直三棱柱ABC![]() 中,AC=3,BC=4,AB=5,A
中,AC=3,BC=4,AB=5,A![]() =4.
=4.

(1)证明:![]() ;
;
(2)求二面角![]() 的余弦值大小.
的余弦值大小.
【答案】⑴见证明;⑵![]()
【解析】
(1)根据AC,BC,CC1两两垂直,建立如图以C为坐标原点,建立空间直角坐标系C﹣xyz,写出要用的点的坐标,根据两个向量的数量级等于0,证出两条线段垂直.
(2)根据所给的两个平面的法向量一个可以直接看出另一个设出根据数量级等于0,求出结果,根据两个平面的法向量所成的角求出两个平面所成的角.
∵直三棱柱ABC﹣A1B1C1,底面三边长AC=3,BC=4,AB=5,
∴AC,BC,CC1两两垂直.
如图以C为坐标原点,建立空间直角坐标系C﹣xyz,则C(0,0,0),A(3,0,0),C1(0,0,4),B(0,4,0),B1(0,4,4). …(2分)
证明:(1)∵![]() =(﹣3,0,0),
=(﹣3,0,0),![]() =(0,﹣4,4),
=(0,﹣4,4),
∴![]()
![]() =0,
=0,
故AC⊥BC1…(4分)
解:(2)平面ABC的一个法向量为![]() =(0,0,1),
=(0,0,1),
设平面C1AB的一个法向量为![]() =(x,y,z),
=(x,y,z),
![]() =(﹣3,0,4),
=(﹣3,0,4),![]() =(﹣3,4,0),
=(﹣3,4,0),
由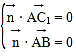 得:
得:![]() …(6分)
…(6分)
令x=4,则z=3,y=3则![]() =(4,3,3).…(7分)
=(4,3,3).…(7分)
故cos<![]() ,
,![]() >=
>=![]() =
=![]() .
.
即二面角![]() ABC的余弦值为
ABC的余弦值为![]() .
.


科目:高中数学 来源: 题型:
【题目】已知定义[x]表示不超过的最大整数,如[2]=2,[2,2]=2,执行如图所示的程序框图,则输出S=( ) 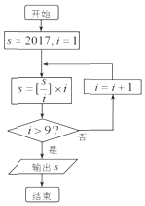
A.1991
B.2000
C.2007
D.2008
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在四棱锥P﹣ABCD中,平面PAD⊥平面ABCD,PA⊥BC,E是棱PC的中点,∠DAB=90°,AB∥CD,AD=CD=2AB=2.
(Ⅰ)求证:PA⊥平面ABCD;
(Ⅱ)若二面角E﹣BD﹣P大于60°,求四棱锥P﹣ABCD体积的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知圆![]() 与直线
与直线![]() ,且直线
,且直线![]() 有唯一的一个点
有唯一的一个点![]() ,使得过
,使得过![]() 点作圆
点作圆![]() 的两条切线互相垂直,则
的两条切线互相垂直,则![]() _____;设
_____;设![]() 是直线
是直线![]() 上的一条线段,若对于圆
上的一条线段,若对于圆![]() 上的任意一点
上的任意一点![]() ,则
,则![]() 的最小值_____.
的最小值_____.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知命题p:不等式ax2+ax+1>0的解集为R,则实数a∈(0,4);命题q“x2﹣2x﹣8>0”是“x>5”的必要不充分条件,则下列命题正确的是( )
A.p∧q
B.p∧(¬q)
C.(¬p)∧(¬q)
D.(¬p)∧q
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=( ![]() )ax , a为常数,且函数的图象过点(﹣1,2).
)ax , a为常数,且函数的图象过点(﹣1,2).
(1)求a的值;
(2)若g(x)=4﹣x﹣2,且g(x)=f(x),求满足条件的x的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某城市为了解游客人数的变化规律,提高旅游服务质量,收集并整理了2014年1月至2016年12月期间月接待游客量(单位:万人)的数据,绘制了下面的折线图.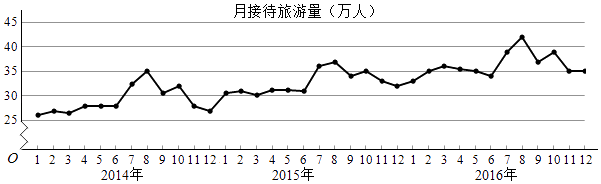
根据该折线图,下列结论错误的是( )
A.月接待游客量逐月增加
B.年接待游客量逐年增加
C.各年的月接待游客量高峰期大致在7,8月
D.各年1月至6月的月接待游客量相对于7月至12月,波动性更小,变化比较平稳
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com