
【题目】设![]() 是自然对数的底数,函数
是自然对数的底数,函数![]() 有零点,且所有零点的和不大于6,则
有零点,且所有零点的和不大于6,则![]() 的取值范围为______.
的取值范围为______.
【答案】![]()
【解析】
对![]() 分四种情况讨论,分别判断函数的单调性与最值,根据单调性、最值,判断函数是否有零点,若函数有零点,判断所有零点的和是否不大于6,综合各种讨论结果,即可得结论.
分四种情况讨论,分别判断函数的单调性与最值,根据单调性、最值,判断函数是否有零点,若函数有零点,判断所有零点的和是否不大于6,综合各种讨论结果,即可得结论.
①![]() ,
,
![]() 时,
时,![]() 在
在![]() 单调递减,
单调递减,
且![]() 在
在![]() 有一个小于0的零点;
有一个小于0的零点;
![]() 时,
时,![]() 在
在![]() 单调递增,
单调递增,
![]() ,
,![]() 在
在![]() 有一个小于1的零点,因此满足条件.
有一个小于1的零点,因此满足条件.
②![]()
(1)![]() 时,
时,![]() 在
在![]() 单调递减,
单调递减,
![]() 在
在![]() 上没有零点.
上没有零点.
又![]() ,故
,故![]() 在
在![]() 上也没有零点,因此不满足题意.
上也没有零点,因此不满足题意.
(2)![]() 时,
时,![]() 在
在![]() 上单调递减,在
上单调递减,在![]() 上单调递增,
上单调递增,
![]() 在
在![]() 上没有零点.
上没有零点.
又![]() ,故
,故![]() 在
在![]() 上也没有零点,因此不满足题意.
上也没有零点,因此不满足题意.
(3)![]() 时,
时,![]() 在
在 ![]() 上没有零点,
上没有零点,
![]() 在
在![]() 上只有零点2,满足条件.
上只有零点2,满足条件.
(4)![]() 时,
时,![]() 在
在![]() 上没有零点,在
上没有零点,在![]() 上有两个不相等的零点,
上有两个不相等的零点,
且和为![]() ,故满足题意的范围是
,故满足题意的范围是![]() .
.
综上所述,![]() 的取值范围为
的取值范围为![]() ,故答案为
,故答案为![]() .
.


 智趣寒假作业云南科技出版社系列答案
智趣寒假作业云南科技出版社系列答案科目:高中数学 来源: 题型:
【题目】选修4-4:坐标系与参数方程
在直角坐标系![]() 中,直线
中,直线![]() 的参数方程为
的参数方程为![]() (
(![]() 为参数).以坐标原点为极点,
为参数).以坐标原点为极点,![]() 轴的正半轴为极轴建立极坐标系,曲线
轴的正半轴为极轴建立极坐标系,曲线![]() 的极坐标方程为
的极坐标方程为![]() .
.
(1)若曲线![]() 上一点
上一点![]() 的极坐标为
的极坐标为![]() ,且
,且![]() 过点
过点![]() ,求
,求![]() 的普通方程和
的普通方程和![]() 的直角坐标方程;
的直角坐标方程;
(2)设点![]() ,
,![]() 与
与![]() 的交点为
的交点为![]() ,求
,求![]() 的最大值.
的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】下面有五个命题:
①函数y=sin4x-cos4x的最小正周期是![]() ;
;
②终边在y轴上的角的集合是{α|α=![]() ;
;
③在同一坐标系中,函数y=sinx的图象和函数y=x的图象有三个公共点;
④把函数![]() ;
;
⑤函数![]() 。
。
其中真命题的序号是__________(写出所有真命题的编号)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】下列说法中正确的个数是( )
①球的半径是球面上任意一点与对球心的连线;
②球面上任意两点的连线是球的直径;
③用一个平面截一个球,得到的截面是一个圆;
④用一个平面截一个球,得到的截面是一个圆面;
⑤以半圆的直径所在直线为轴旋转形成的曲面叫做球;
⑥空间中到定点的距离等于定长的所有的点构成的曲面是球面.
A.0B.1C.2D.3
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在平面直角坐标系![]() 中,角
中,角![]() 以
以![]() 为始边,终边与单位圆
为始边,终边与单位圆![]() 相交于点
相交于点![]() .过点
.过点![]() 的圆
的圆![]() 的切线交
的切线交![]() 轴于点
轴于点![]() ,点
,点![]() 的横坐标关于角
的横坐标关于角![]() 的函数记为
的函数记为![]() . 则下列关于函数
. 则下列关于函数![]() 的说法正确的( )
的说法正确的( )

A. ![]() 的定义域是
的定义域是![]()
B. ![]() 的图象的对称中心是
的图象的对称中心是![]()
C. ![]() 的单调递增区间是
的单调递增区间是![]()
D. ![]() 对定义域内的
对定义域内的![]() 均满足
均满足![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】一个盒子中装有6张卡片,上面分别写着如下六个定义域为![]() 的函数:
的函数:![]() ,
, ![]() ,
,![]() ,
, ![]() ,
,![]() ,
,![]() 从盒子中任取2张卡片,将卡片上的函数相乘得到一个新函数,所得新函数为奇函数的概率是 __________.
从盒子中任取2张卡片,将卡片上的函数相乘得到一个新函数,所得新函数为奇函数的概率是 __________.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】每年10月中上旬是小麦的最佳种植时间,但小麦的发芽会受到土壤、气候等多方面因素的影响.某科技小组为了解昼夜温差的大小与小麦发芽的多少之间的关系,在不同的温差下统计了100颗小麦种子的发芽数,得到了如下数据:
温差 | 8 | 10 | 11 | 12 | 13 |
发芽数 | 79 | 81 | 85 | 86 | 90 |
(1)请根据统计的最后三组数据,求出![]() 关于
关于![]() 的线性回归方程
的线性回归方程![]() ;
;
(2)若由(1)中的线性回归方程得到的估计值与前两组数据的实际值误差均不超过两颗,则认为线性回归方程是可靠的,试判断(1)中得到的线性回归方程是否可靠;
(3)若100颗小麦种子的发芽率为![]() 颗,则记为
颗,则记为![]() 的发芽率,当发芽率为
的发芽率,当发芽率为![]() 时,平均每亩地的收益为
时,平均每亩地的收益为![]() 元,某农场有土地10万亩,小麦种植期间昼夜温差大约为
元,某农场有土地10万亩,小麦种植期间昼夜温差大约为![]() ,根据(1)中得到的线性回归方程估计该农场种植小麦所获得的收益.
,根据(1)中得到的线性回归方程估计该农场种植小麦所获得的收益.
附:在线性回归方程![]() 中,
中,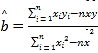 .
.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com