
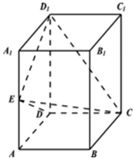
 (Ⅰ)证明:A1B1∥平面CDE;
(Ⅰ)证明:A1B1∥平面CDE;分析 (Ⅰ)证明A1B1∥CD,即可证明:A1B1∥平面CDE;
(Ⅱ)证明:D1E⊥DE,CD⊥D1E,CD∩DE=D,即可证明D1E⊥平面CDE;
(Ⅲ)三棱锥D1-CDE的体积=$\frac{1}{3}•{D}_{1}E•\frac{1}{2}CD•ED$,即可求三棱锥D1-CDE的体积.
解答 (Ⅰ)证明:∵ABCD-A1B1C1D1是长方体,
∴A1B1∥CD,
∵A1B1?平面CDE,CD?平面CDE,
∴A1B1∥平面CDE;
(Ⅱ)证明:∵AB=BC=$\frac{1}{2}A{A}_{1}$=a,E是AA1中点,
∴D1E=DE=$\sqrt{2}$a,
△DD1E中,D1E2+DE2=DD12
∴∠D1ED=90°,
∴D1E⊥DE,
∵CD⊥D1E,CD∩DE=D
∴D1E⊥平面CDE;
(Ⅲ)解:由(Ⅱ)D1E⊥平面CDE,可得D1E是三棱锥D1-CDE的高,
∴三棱锥D1-CDE的体积=$\frac{1}{3}•{D}_{1}E•\frac{1}{2}CD•ED$=$\frac{1}{3}•\sqrt{2}a•\frac{1}{2}•a•\sqrt{2}a$=$\frac{1}{3}{a}^{3}$.
点评 本题考查线面平行、垂直的判定,考查三棱锥D1-CDE的体积,考查学生分析解决问题的能力,属于中档题.


科目:高中数学 来源: 题型:选择题
| A. | F=G | B. | F⊆G | C. | G⊆F | D. | F∪G=G |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
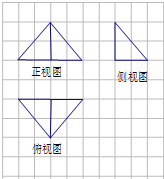
| A. | $\frac{8}{3}π$ | B. | 8π | C. | $\frac{32}{3}π$ | D. | $\frac{16}{3}π$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题

查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com