
”¾ĢāÄæ”æĪŖĮĖŠū“«½ńÄź10ŌĀŌŚÄ³ŹŠ¾ŁŠŠµÄ”°µŚŹ®½ģÖŠ¹śŅÕŹõ½Ś”±£¬”°Ź®ŅÕ½Ś”±³ļĪÆ»į¾Ł°ģĮĖ”°Ź®ŅÕ½Ś”±ÖŖŹ¶ÓŠ½±ĪŹ“š»ī¶Æ£¬Ė껜¶ŌŹŠĆń15”«65ĖźµÄČĖČŗ³éŃł![]() ČĖ£¬»Ų“šĪŹĢāĶ³¼Ę½į¹ūČēĻĀĶ¼±ķĖłŹ¾£ŗ
ČĖ£¬»Ų“šĪŹĢāĶ³¼Ę½į¹ūČēĻĀĶ¼±ķĖłŹ¾£ŗ
×éŗÅ | ·Ö×é | »Ų“šÕżČ·µÄČĖŹż | »Ų“šÕżČ·µÄČĖŹżÕ¼±¾×éµÄʵĀŹ | ʵĀŹ·Ö²¼Ö±·½Ķ¼ |
µŚ1×é |
| 5 | 0.5 |
|
µŚ2×é |
|
| 0.9 | |
µŚ3×é |
| 27 |
| |
µŚ4×é |
| 9 | 0.36 | |
µŚ5×é |
| 3 | 0.2 |
£Ø1£©·Ö±šĒó³ö![]() µÄÖµ£»
掙术
£Ø2£©“ÓµŚ2£¬3£¬4×é»Ų“šÕżČ·µÄČĖÖŠÓĆ·Ö²ć³éŃłµÄ·½·Ø³éČ”6ČĖ£¬”°Ź®ŅÕ½Ś”±³ļĪÆ»į¾ö¶ØŌŚĖł³éČ”µÄ6ČĖÖŠĖ껜³éČ”2ČĖ°ä·¢ŠŅŌĖ½±£¬ĒóĖł³éČ”µÄČĖÖŠµŚ2×éÖĮÉŁÓŠ1ČĖ»ńµĆŠŅŌĖ½±µÄøÅĀŹ.
”¾“š°ø”æ£Ø1£©18£»0.9£Ø2£©![]()
”¾½āĪö”æ
£Ø1£©øł¾ŻĘµĀŹ±ķæɵƵŚ1×éČĖŹżĪŖ![]() £¬ŌŁ½įŗĻʵĀŹ·Ö²¼Ö±·½Ķ¼
£¬ŌŁ½įŗĻʵĀŹ·Ö²¼Ö±·½Ķ¼![]() £¬½ų¶ųæÉĒó³ö
£¬½ų¶ųæÉĒó³ö![]() µÄÖµ
µÄÖµ
£Ø2£©øł¾Ż·Ö²ć³éŃłĖć³öø÷×é³éČ”µÄČĖŹż£¬ĮŠ¾Ł³öĖłÓŠµÄ»ł±¾ŹĀ¼ž£¬ŌŁĒó³öĖł³éČ”µÄČĖÖŠµŚ2×éÖĮÉŁÓŠ1ČĖ»ńµĆŠŅŌĖ½±µÄĒéæö£¬ĄūÓĆ¹ÅµäøÅŠĶµÄøÅĀŹ¼ĘĖć¹«Ź½¼“æÉĒó½ā.
£Ø1£©ÓÉʵĀŹ±ķÖŠµŚ1×鏿¾ŻæÉÖŖ£¬µŚ1×é×ÜČĖŹżĪŖ![]() £¬
£¬
ŌŁ½įŗĻʵĀŹ·Ö²¼Ö±·½Ķ¼æÉÖŖ![]() £¬
£¬
![]() £¬
£¬![]() .
.
£Ø2£©µŚ2£¬3£¬4×éÖŠ»Ų“šÕżČ·µÄ¹²ÓŠ54ČĖ.
”ąĄūÓĆ·Ö²ć³éŃłŌŚ54ČĖÖŠ³éČ”6ČĖ£¬
Ćæ×é·Ö±š³éČ”µÄČĖŹżĪŖ£ŗµŚ2×é£ŗ![]() ČĖ£¬
ČĖ£¬
µŚ3×é£ŗ![]() ČĖ£¬
ČĖ£¬
µŚ4×é£ŗ![]() ČĖ.
ČĖ.
É赌2×éµÄ2ČĖĪŖ![]() £¬µŚ3×éµÄ3ČĖĪŖ
£¬µŚ3×éµÄ3ČĖĪŖ![]() £¬
£¬
µŚ4×éµÄ1ČĖĪŖ![]() £¬Ōņ“Ó6ČĖÖŠ³é2ČĖĖłÓŠæÉÄܵĽį¹ūÓŠ£ŗ
£¬Ōņ“Ó6ČĖÖŠ³é2ČĖĖłÓŠæÉÄܵĽį¹ūÓŠ£ŗ
![]() £¬
£¬![]() £¬
£¬![]() £¬
£¬![]() £¬
£¬![]() £¬
£¬![]() £¬
£¬
![]() £¬
£¬![]() £¬
£¬![]() £¬
£¬![]() £¬
£¬![]() £¬
£¬![]() £¬
£¬
![]() £¬
£¬![]() £¬
£¬![]() £¬¹²15øö»ł±¾ŹĀ¼ž£¬
£¬¹²15øö»ł±¾ŹĀ¼ž£¬
ĘäÖŠµŚ2×éÖĮÉŁÓŠ1ČĖ±»³éÖŠµÄÓŠ![]() £¬
£¬![]() £¬
£¬![]() £¬
£¬
![]() £¬
£¬![]() £¬
£¬![]() £¬
£¬![]() £¬
£¬![]() £¬
£¬![]() Õā9øö»ł±¾ŹĀ¼ž.
Õā9øö»ł±¾ŹĀ¼ž.
”ąµŚ2×éÖĮÉŁÓŠ1ČĖ»ńµĆŠŅŌĖ½±µÄøÅĀŹĪŖ![]() .
.



| Äź¼¶ | øßÖŠæĪ³Ģ | Äź¼¶ | ³õÖŠæĪ³Ģ |
| øßŅ» | øßŅ»Ćā·ŃæĪ³ĢĶĘ¼ö£” | ³õŅ» | ³õŅ»Ćā·ŃæĪ³ĢĶĘ¼ö£” |
| ø߶ž | ø߶žĆā·ŃæĪ³ĢĶĘ¼ö£” | ³õ¶ž | ³õ¶žĆā·ŃæĪ³ĢĶĘ¼ö£” |
| øßČż | øßČżĆā·ŃæĪ³ĢĶĘ¼ö£” | ³õČż | ³õČżĆā·ŃæĪ³ĢĶĘ¼ö£” |
æĘÄæ£ŗøßÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
”¾ĢāÄæ”æŌŚĖÄĄā׶P©ABCDÖŠ£¬µ×ĆęABCDŹĒ±ß³¤ĪŖ4µÄÕż·½ŠĪ£¬”÷PADŹĒŅ»øöÕżČż½ĒŠĪ£¬ČōĘ½ĆęPAD”ĶĘ½ĆęABCD£¬ŌņøĆĖÄĄā׶µÄĶā½ÓĒņµÄ±ķĆ껿ĪŖ_____.
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗøßÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
”¾ĢāÄæ”æŌŚÖ±½Ē×ų±źĻµ![]() ÖŠ£¬ĒśĻß
ÖŠ£¬ĒśĻß![]() µÄ²ĪŹż·½³ĢĪŖ
µÄ²ĪŹż·½³ĢĪŖ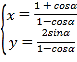 (
(![]() ĪŖ²ĪŹż).ŅŌ
ĪŖ²ĪŹż).ŅŌ![]() ĪŖ¼«µć£¬
ĪŖ¼«µć£¬![]() ÖįµÄÕż°ėÖįĪŖ¼«Öį½ØĮ¢¼«×ų±źĻµ£¬Ö±Ļß
ÖįµÄÕż°ėÖįĪŖ¼«Öį½ØĮ¢¼«×ų±źĻµ£¬Ö±Ļß![]() µÄ¼«×ų±ź·½³ĢĪŖ
µÄ¼«×ų±ź·½³ĢĪŖ![]() (
(![]() )£¬½«ĒśĻß
)£¬½«ĒśĻß![]() Ļņ×óĘ½ŅĘ2øöµ„Ī»³¤¶ČµĆµ½ĒśĻß
Ļņ×óĘ½ŅĘ2øöµ„Ī»³¤¶ČµĆµ½ĒśĻß![]() .
.
£Ø1£©ĒóĒśĻß![]() µÄĘÕĶØ·½³ĢŗĶ¼«×ų±ź·½³Ģ£»
µÄĘÕĶØ·½³ĢŗĶ¼«×ų±ź·½³Ģ£»
£Ø2£©ÉčÖ±Ļß![]() ÓėĒśĻß
ÓėĒśĻß![]() ½»ÓŚ
½»ÓŚ![]() Į½µć£¬Ēó
Į½µć£¬Ēó![]() µÄȔֵ·¶Ī§.
µÄȔֵ·¶Ī§.
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗøßÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
”¾ĢāÄæ”收¾ÅÕĀĖćŹõ”·ŹĒĪŅ¹ś¹Å“śŹżŃ§³É¾ĶµÄ½Ü³ö“ś±ķ.ĘäÖŠ”¶·½Ģļ”·ÕĀøų³ö¼ĘĖć»”ĢļĆ껿µÄ¾Ń鹫Ź½ĪŖ£ŗ![]() .»”Ģļ£ØČēĶ¼1ŅõÓ°²æ·Ö£©ÓÉŌ²»”ŗĶĘäĖł¶ŌĻŅĪ§³É£¬ĻŅ”±ÖøŌ²»”Ėł¶ŌĻŅ³¤£¬”°Źø”±µČÓŚ°ė¾¶³¤ÓėŌ²ŠÄµ½ĻŅµÄ¾ąĄėÖ®²ī.Ąą±Č»”ĢļĆ껿¹«Ź½µĆµ½Ēņȱ(ČēĶ¼ 2)½üĖĘĢå»ż¹«Ź½£ŗ
.»”Ģļ£ØČēĶ¼1ŅõÓ°²æ·Ö£©ÓÉŌ²»”ŗĶĘäĖł¶ŌĻŅĪ§³É£¬ĻŅ”±ÖøŌ²»”Ėł¶ŌĻŅ³¤£¬”°Źø”±µČÓŚ°ė¾¶³¤ÓėŌ²ŠÄµ½ĻŅµÄ¾ąĄėÖ®²ī.Ąą±Č»”ĢļĆ껿¹«Ź½µĆµ½Ēņȱ(ČēĶ¼ 2)½üĖĘĢå»ż¹«Ź½£ŗ![]() Ō²Ć껿
Ō²Ć껿![]() Źø
Źø![]() .ĒņȱŹĒÖøŅ»øöĒņ±»Ę½Ćę½ŲĻĀµÄŅ»²æ·Ö£¬ĻĆĆżĪøżĢåÓż¹Ż½üĖĘĒņȱ½į¹¹£ØČēĶ¼3)£¬ČōøĆĢåÓż¹ŻÕ¼µŲĆ껿Ō¼ĪŖ18000
.ĒņȱŹĒÖøŅ»øöĒņ±»Ę½Ćę½ŲĻĀµÄŅ»²æ·Ö£¬ĻĆĆżĪøżĢåÓż¹Ż½üĖĘĒņȱ½į¹¹£ØČēĶ¼3)£¬ČōøĆĢåÓż¹ŻÕ¼µŲĆ껿Ō¼ĪŖ18000![]() £¬½Ø֞ȯ»żŌ¼ĪŖ340000
£¬½Ø֞ȯ»żŌ¼ĪŖ340000![]() £¬¹Ą¼ĘĢåÓż¹Ż½ØÖžø߶Č(µ„Ī»£ŗ
£¬¹Ą¼ĘĢåÓż¹Ż½ØÖžø߶Č(µ„Ī»£ŗ![]() )ĖłŌŚĒų¼äĪŖ£Ø £©
)ĖłŌŚĒų¼äĪŖ£Ø £©
²Īæ¼Źż¾Ż: ![]() £¬
£¬![]() £¬
£¬![]() £¬
£¬
![]() £¬
£¬![]() .
.



A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗøßÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
”¾ĢāÄæ”æČēĶ¼ĖłŹ¾£¬ĖÄĄā׶![]() µÄ²ąĆę
µÄ²ąĆę![]() µ×Ćę
µ×Ćę![]() £¬µ×Ćę
£¬µ×Ćę![]() ŹĒÖ±½ĒĢŻŠĪ£¬ĒŅ
ŹĒÖ±½ĒĢŻŠĪ£¬ĒŅ![]() ,
, ![]() ,
, ![]() ŹĒ
ŹĒ![]() ÖŠµć.
ÖŠµć.
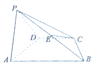
£Ø1£©ĒóÖ¤£ŗ ![]() Ę½Ćę
Ę½Ćę![]() £»
£»
£Ø2£©Čō![]() £¬ĒóÖ±Ļß
£¬ĒóÖ±Ļß![]() ÓėĘ½Ćę
ÓėĘ½Ćę![]() Ėł³É½ĒµÄ“óŠ”.
Ėł³É½ĒµÄ“óŠ”.
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗøßÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
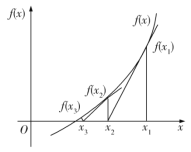
”¾ĢāÄæ”æÅ£¶Łµü“ś·Ø£ØNewton's method£©ÓÖ³ĘÅ£¶ŁØCĄ·ņŃ··½·Ø£ØNewtonØCRaphsonmethod£©£¬ŹĒÅ£¶ŁŌŚ17ŹĄ¼ĶĢį³öµÄŅ»ÖÖ½üĖĘĒó·½³ĢøłµÄ·½·Ø.ČēĶ¼£¬Éč![]() ŹĒ
ŹĒ![]() µÄøł£¬Ń”Č”
µÄøł£¬Ń”Č”![]() ×÷ĪŖ
×÷ĪŖ![]() ³õŹ¼½üĖĘÖµ£¬¹żµć
³õŹ¼½üĖĘÖµ£¬¹żµć![]() ×÷ĒśĻß
×÷ĒśĻß![]() µÄĒŠĻß
µÄĒŠĻß![]() Óė
Óė![]() ÖįµÄ½»µćµÄŗį×ų±ź
ÖįµÄ½»µćµÄŗį×ų±ź![]() £¬³Ę
£¬³Ę![]() ŹĒ
ŹĒ![]() µÄŅ»“Ī½üĖĘÖµ£¬¹żµć
µÄŅ»“Ī½üĖĘÖµ£¬¹żµć![]() ×÷ĒśĻß
×÷ĒśĻß![]() µÄĒŠĻߣ¬ŌņøĆĒŠĻßÓė
µÄĒŠĻߣ¬ŌņøĆĒŠĻßÓė![]() ÖįµÄ½»µćµÄŗį×ų±źĪŖ
ÖįµÄ½»µćµÄŗį×ų±źĪŖ![]() £¬³Ę
£¬³Ę![]() ŹĒ
ŹĒ![]() µÄ¶ž“Ī½üĖĘÖµ.ÖŲø“ŅŌÉĻ¹ż³Ģ£¬Ö±µ½
µÄ¶ž“Ī½üĖĘÖµ.ÖŲø“ŅŌÉĻ¹ż³Ģ£¬Ö±µ½![]() µÄ½üĖĘÖµ×ć¹»Š”£¬¼“°Ń
µÄ½üĖĘÖµ×ć¹»Š”£¬¼“°Ń![]() ×÷ĪŖ
×÷ĪŖ![]() µÄ½üĖĘ½ā.Éč
µÄ½üĖĘ½ā.Éč![]() ¹¹³ÉŹżĮŠ
¹¹³ÉŹżĮŠ![]() .¶ŌÓŚĻĀĮŠ½įĀŪ£ŗ
.¶ŌÓŚĻĀĮŠ½įĀŪ£ŗ
¢Ł![]() £»
£»
¢Ś![]() £»
£»
¢Ū![]() £»
£»
¢Ü![]() .
.
ĘäÖŠÕżČ·½įĀŪµÄŠņŗÅĪŖ__________£®
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗøßÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
”¾ĢāÄæ”æ½üÄźĄ“£¬ŠĀÄÜŌ“Ęū³µ¼¼Źõ²»¶ĻĶĘ³Ā³öŠĀ£¬ŠĀ²śĘ·²»¶ĻÓæĻÖ£¬ŌŚĘū³µŹŠ³”ÉĻÓ°ĻģĮ¦²»¶ĻŌö“ó.¶ÆĮ¦Šīµē³Ų¼¼Źõ×÷ĪŖŠĀÄÜŌ“Ęū³µµÄŗĖŠÄ¼¼Źõ£¬ĖüµÄ²»¶Ļ³ÉŹģŅ²ŹĒĶĘ¶ÆŠĀÄÜŌ“Ęū³µ·¢Õ¹µÄÖ÷ŅŖ¶ÆĮ¦.¼Ł¶ØĻÖŌŚŹŠŹŪµÄijæīŠĀÄÜŌ“Ęū³µÉĻ£¬³µŌŲ¶ÆĮ¦Šīµē³Ų³ä·ÅµēŃ»·“ĪŹż“ļµ½2000“ĪµÄøÅĀŹĪŖ85%£¬³ä·ÅµēŃ»·“ĪŹż“ļµ½2500“ĪµÄøÅĀŹĪŖ35%.ČōijÓĆ»§µÄ×ŌÓĆŠĀÄÜŌ“Ęū³µŅŃ¾¾¹żĮĖ2000“Ī³äµē£¬ÄĒĆ“ĖūµÄ³µÄܹ»³äµē2500“ĪµÄøÅĀŹĪŖ______.
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗøßÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
”¾ĢāÄæ”æŅŃÖŖŗÆŹż![]() £ØkĪŖ³£Źż£¬
£ØkĪŖ³£Źż£¬![]() ĒŅ
ĒŅ![]() £©£®
£©£®
£Ø1£©ŌŚĻĀĮŠĢõ¼žÖŠŃ”ŌńŅ»øö________Ź¹ŹżĮŠ![]() ŹĒµČ±ČŹżĮŠ£¬ĖµĆ÷ĄķÓÉ£»
ŹĒµČ±ČŹżĮŠ£¬ĖµĆ÷ĄķÓÉ£»
¢ŁŹżĮŠ![]() ŹĒŹ×ĻīĪŖ2£¬¹«±ČĪŖ2µÄµČ±ČŹżĮŠ£»
ŹĒŹ×ĻīĪŖ2£¬¹«±ČĪŖ2µÄµČ±ČŹżĮŠ£»
¢ŚŹżĮŠ![]() ŹĒŹ×ĻīĪŖ4£¬¹«²īĪŖ2µÄµČ²īŹżĮŠ£»
ŹĒŹ×ĻīĪŖ4£¬¹«²īĪŖ2µÄµČ²īŹżĮŠ£»
¢ŪŹżĮŠ![]() ŹĒŹ×ĻīĪŖ2£¬¹«²īĪŖ2µÄµČ²īŹżĮŠµÄĒ°nĻīŗĶ¹¹³ÉµÄŹżĮŠ£®
ŹĒŹ×ĻīĪŖ2£¬¹«²īĪŖ2µÄµČ²īŹżĮŠµÄĒ°nĻīŗĶ¹¹³ÉµÄŹżĮŠ£®
£Ø2£©ŌŚ£Ø1£©µÄĢõ¼žĻĀ£¬µ±![]() Ź±£¬Éč
Ź±£¬Éč![]() £¬ĒóŹżĮŠ
£¬ĒóŹżĮŠ![]() µÄĒ°nĻīŗĶ
µÄĒ°nĻīŗĶ![]() .
.
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗøßÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
”¾ĢāÄæ”æ“óŌ¼ŌŚ20ŹĄ¼Ķ30Äź“ś£¬ŹĄ½ēÉĻŠķ¶ą¹ś¼Ņ¶¼Į÷“«×ÅÕāŃłŅ»øöĢāÄæ£ŗČĪČ”Ņ»øöÕżÕūŹż![]() £¬Čē¹ūĖüŹĒżŹż£¬Ōņ³żŅŌ2£»Čē¹ūĖüŹĒĘꏿ£¬Ōņ½«Ėü³ĖŅŌ3¼Ó1£¬ÕāŃł·“ø“ŌĖĖć£¬×īŗó½į¹ū±ŲČ»ŹĒ1.ÕāøöĢāÄæŌŚ¶«·½±»³ĘĪŖ”°½Ē¹Č²ĀĻė”±£¬ŹĄ½ēŅ»Į÷µÄ“óŹżŃ§¼Ņ¶¼±»Ęä¾ķČėĘäÖŠ£¬ÓĆ¾”ĮĖø÷ÖÖ·½·Ø£¬ÉõÖĮ¶ÆÓĆĮĖ×īĻČ½ųµÄµē×Ó¼ĘĖ滜£¬ŃéĖćµ½¶Ō700ŅŚŅŌÄŚµÄ×ŌČ»ŹżÉĻŹö½įĀŪ¾łĪŖÕżČ·µÄ£¬µ«Č“øų²»³öŅ»°ćŠŌµÄÖ¤Ć÷.ĄżČēČ”
£¬Čē¹ūĖüŹĒżŹż£¬Ōņ³żŅŌ2£»Čē¹ūĖüŹĒĘꏿ£¬Ōņ½«Ėü³ĖŅŌ3¼Ó1£¬ÕāŃł·“ø“ŌĖĖć£¬×īŗó½į¹ū±ŲČ»ŹĒ1.ÕāøöĢāÄæŌŚ¶«·½±»³ĘĪŖ”°½Ē¹Č²ĀĻė”±£¬ŹĄ½ēŅ»Į÷µÄ“óŹżŃ§¼Ņ¶¼±»Ęä¾ķČėĘäÖŠ£¬ÓĆ¾”ĮĖø÷ÖÖ·½·Ø£¬ÉõÖĮ¶ÆÓĆĮĖ×īĻČ½ųµÄµē×Ó¼ĘĖ滜£¬ŃéĖćµ½¶Ō700ŅŚŅŌÄŚµÄ×ŌČ»ŹżÉĻŹö½įĀŪ¾łĪŖÕżČ·µÄ£¬µ«Č“øų²»³öŅ»°ćŠŌµÄÖ¤Ć÷.ĄżČēČ”![]() £¬ŌņŅŖĻėĖć³ö½į¹ū1£¬¹²ŠčŅŖ¾¹żµÄŌĖĖć²½ŹżŹĒ£Ø £©
£¬ŌņŅŖĻėĖć³ö½į¹ū1£¬¹²ŠčŅŖ¾¹żµÄŌĖĖć²½ŹżŹĒ£Ø £©
A.9B.10C.11D.12
²éæ““š°øŗĶ½āĪö>>
°Ł¶ČÖĀŠÅ - Į·Ļ°²įĮŠ±ķ - ŹŌĢāĮŠ±ķ
ŗž±±Ź”»„ĮŖĶųĪ„·ØŗĶ²»Į¼ŠÅĻ¢¾Ł±ØĘ½ĢØ | ĶųÉĻÓŠŗ¦ŠÅĻ¢¾Ł±Ø×ØĒų | µēŠÅÕ©Ę¾Ł±Ø×ØĒų | É꥜Ź·ŠéĪŽÖ÷ŅåÓŠŗ¦ŠÅĻ¢¾Ł±Ø×ØĒų | ÉęĘóĒÖČؾŁ±Ø×ØĒų
Ī„·ØŗĶ²»Į¼ŠÅĻ¢¾Ł±Øµē»°£ŗ027-86699610 ¾Ł±ØÓŹĻä£ŗ58377363@163.com