
如图,过半径为R的球面上一点P作三条两两垂直的弦PA、PB、PC,

(1)求证:PA2+PB2+PC2为定值;
(2)求三棱锥P-ABC的体积的最大值.
解:(1)设过PA、PB的平面截球得⊙O1,∵PA⊥PB,
∴AB是⊙O1的直径,连PO1并延长交⊙O1于D,则PADB是矩形,PD2=PA2+PB2.
设O为球心,则OO1⊥平面⊙O1,
∵PC⊥⊙O1平面,
∴OO1∥PC,因此过PC、PD的平面经过球心O,截球得大圆,又PC⊥PD.
∴CD是球的直径.
故PA2+PB2+PC2=PD2+PC2=CD2=4R2定值.
(2)设PA、PB、PC的长分别为x、y、z,则三棱锥P-ABC的体积V=![]() xyz,
xyz,
V2=![]() x2y2z2≤
x2y2z2≤![]() (
(![]() )3=
)3=![]() ·
·![]() =
=![]() R6.
R6.
∴V≤![]() R3.
R3.
即V最大=![]() R3.
R3.
评析:定值问题可用特殊情况先“探求”,如本题(1)若先考虑PAB是大圆,探求得定值4R2可为(1)的证明指明方向.
球面上任一点对球的直径所张的角等于90°,这应记作很重要的性质.
解析:先选其中两条弦PA、PB,设其确定的平面截球得⊙O1,AB是⊙O1的直径,连PO1并延长交⊙O1于D,PADB是矩形,PD2=AB2=PA2+PB2,然后只要证得PC和PD确定是大圆就可以了.


科目:高中数学 来源: 题型:
 如图,在半径为3的球面上有A、B、C三点,∠ABC=90°,BA=BC,球心O到平面ABC的距离是
如图,在半径为3的球面上有A、B、C三点,∠ABC=90°,BA=BC,球心O到平面ABC的距离是3
| ||
| 2 |
A、
| ||
| B、π | ||
C、
| ||
| D、2π |
查看答案和解析>>
科目:高中数学 来源:2011-2012学年重庆49中高三(下)第一次质量抽测数学试卷(理科)(解析版) 题型:填空题
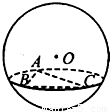 如图,在半径为3的球面上有A、B、C三点,∠ABC=90°,BA=BC,球心O到平面ABC的距离是
如图,在半径为3的球面上有A、B、C三点,∠ABC=90°,BA=BC,球心O到平面ABC的距离是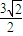 ,则B、C两点的球面距离是 .
,则B、C两点的球面距离是 .查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com