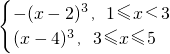Question

定义在R上的函数f（x）满足f（x+2）=-f（x），且当x∈[-1，1]时，f（x）=x³．
（1）求f（x）在[1，5]上的表达式；
（2）若A={x|f（x）＞a，x∈R}，且A≠∅，求实数a的取值范围．

Answer 1

解：由f（x+2）=-f（x），
∴f（x+4）=-f（x+2）=f（x），
故f（x）的周期为4
（1）当x∈[3，5]时，x-4∈[-1，1]，
∴f（x-4）=（x-4）³，
又T=4，
∴f（x）=f（x-4）=（x-4）³，x∈[3，5]
当x∈[1，3）时，x-2∈[-1，1），
∴f（x-2）=（x-2）³，
又f（x+2）=-f（x），
∴f（x）=-f（x-2）=-（x-2）³，x∈[1，3）
故f（x）=
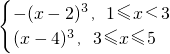
（2）当x∈[1，3）时，f（x）=-（x-2）³为减函数
故f（x）∈（f（3），f（1）]=（-1，1]
当x∈[3，5]时，f（x）=（x-4）³为增函数
故f（x）∈[f（3），f（5）]=[-1，1]
故当x∈[1，5]时，f（x）∈[-1，1]
∵f（x）的周期函数，
∴f（x）的值域为[-1，1]
又∵f（x）＞a，对x∈R有解，
∴a＜1
分析：（1）由已知中函数f（x）满足f（x+2）=-f（x），可得f（x）的周期为4，结合当x∈[-1，1]时，f（x）=x³．可求出当x∈[3，5]时和当x∈[1，3）时的函数解析式，进而得到f（x）在[1，5]上的表达式；
（2）根据f（x）的周期为4，及f（x）在[1，5]上的表达式，我们可以求出函数f（x）的值域，进而根据A={x|f（x）＞a，x∈R}，且A≠∅，可得a小于函数f（x）的最小值，进而得到答案．
点评：本题考查的知识点是函数的周期性，函数的值域，函数的解析式的求法，函数恒成立问题，是函数问题一个相对综合的应用，有一定的难度．