
【题目】在从100到999的所有三位数中,百位、十位、个位数字依次构成等差数列的有__________个;构成等比数列的有__________个.
【答案】45 17
【解析】
利用等差数列与等比数列的定义,通过分类讨论即可得出.
①百位、十位、个位数字依次构成等差数列:公差![]() 时,共有9个:111,……,999.
时,共有9个:111,……,999.
公差![]() 时,共有7个:123,……,789.
时,共有7个:123,……,789.
公差![]() 时,共有5个:135,……,579.
时,共有5个:135,……,579.
公差![]() 时,共有3个:147,258,369.
时,共有3个:147,258,369.
公差![]() 时,共有1个:159.
时,共有1个:159.
同理可得:公差![]() 时,共有8个,987,……,321,210.
时,共有8个,987,……,321,210.
公差![]() 时,共有6个.
时,共有6个.
公差![]() 时,共有4个.
时,共有4个.
公差![]() 时,共有2个.
时,共有2个.
综上共有45个.
②百位、十位、个位数字依次构成等比数列:公比![]() 时,共有9个:111,……,999.
时,共有9个:111,……,999.
公比![]() 时,共有2个:124,248.公比
时,共有2个:124,248.公比![]() 时,共有2个:421,842.
时,共有2个:421,842.
公比![]() 时,共有1个:139.公比
时,共有1个:139.公比![]() 时,共有1个:931.
时,共有1个:931.
公比![]() 时,共有1个:469.公比
时,共有1个:469.公比![]() 时,共有1个:964.
时,共有1个:964.
综上共有:17个.
故答案为45,17.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:
【题目】如图,已知椭圆C:![]() 过原点的直线与椭圆交于A,B两点(点A在第一象限),过点A作x轴的垂线,垂足为点
过原点的直线与椭圆交于A,B两点(点A在第一象限),过点A作x轴的垂线,垂足为点![]() ,设直线BE与椭圆的另一交点为P,连接AP得到直线l,交x轴于点M,交y轴于点N.
,设直线BE与椭圆的另一交点为P,连接AP得到直线l,交x轴于点M,交y轴于点N.
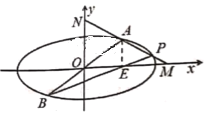
(1)若![]() ,求直线AP的斜率;
,求直线AP的斜率;
(2)记![]() 的面积分别为S1,S2,S3,求
的面积分别为S1,S2,S3,求![]() 的的最大值.
的的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】![]() 年新冠肺炎疫情期间,某区政府为了解本区居民对区政府防疫工作的满意度,从本区居民中随机抽取若干居民进行评分(满分
年新冠肺炎疫情期间,某区政府为了解本区居民对区政府防疫工作的满意度,从本区居民中随机抽取若干居民进行评分(满分![]() 分).根据调查数据制成如下表格和频率分布直方图.已知评分在
分).根据调查数据制成如下表格和频率分布直方图.已知评分在![]() 的居民有
的居民有![]() 人.
人.
满意度评分 |
|
|
|
|
满意度等级 | 不满意 | 基本满意 | 满意 | 非常满意 |
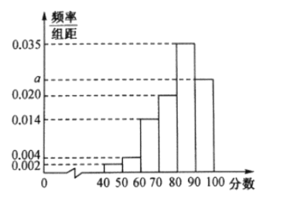
(1)求频率分布直方图中![]() 的值及所调查的总人数;
的值及所调查的总人数;
(2)定义满意度指数![]() (满意程度的平均分)/100,若
(满意程度的平均分)/100,若![]() ,则防疫工作需要进行大的调整,否则不需要大调整.根据所学知识判断该区防疫工作是否需要进行大调整?
,则防疫工作需要进行大的调整,否则不需要大调整.根据所学知识判断该区防疫工作是否需要进行大调整?
(3)为了解部分居民不满意的原因,从不满意的居民(评分在![]() 、
、![]() )中用分层抽样的方法抽取
)中用分层抽样的方法抽取![]() 名居民,倾听他们的意见,并从
名居民,倾听他们的意见,并从![]() 人中抽取
人中抽取![]() 人担任防疫工作的监督员,求这
人担任防疫工作的监督员,求这![]() 人中仅有一人对防疫工作的评分在
人中仅有一人对防疫工作的评分在![]() 内的概率.
内的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设n为正整数,集合A=![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() .对于集合A中的任意元素
.对于集合A中的任意元素![]() 和
和![]() ,记
,记![]() .
.
(Ⅰ)当n=3时,若![]() ,
,![]() ,求
,求![]() 和
和![]() 的值;
的值;
(Ⅱ)当![]() 时,对于
时,对于![]() 中的任意两个不同的元素
中的任意两个不同的元素![]() ,
,![]() ,证明:
,证明:![]() .
.
(Ⅲ)给定不小于2的正整数n,设B是A的子集,且满足:对于B中的任意两个不同元素![]() ,
,![]() ,
,![]() .写出一个集合B,使其元素个数最多,并说明由.
.写出一个集合B,使其元素个数最多,并说明由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知四面体![]() 中,
中,![]() ,
,![]() ,
,![]() ,
,![]() 为其外接球球心,
为其外接球球心,![]() 与
与![]() ,
,![]() ,
,![]() 所成的角分别为
所成的角分别为![]() ,
,![]() ,
,![]() .有下列结论:
.有下列结论:
①该四面体的外接球的表面积为![]() ,
,
②该四面体的体积为10,
③![]()
④![]()
其中所有正确结论的编号为___________
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】高二某班共有45人,学号依次为1、2、3、…、45,现按学号用系统抽样的办法抽取一个容量为5的样本,已知学号为6、24、33的同学在样本中,那么样本中还有两个同学的学号应为( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=xlnx+2x﹣1.
(1)求f(x)的极值;
(2)若对任意的x>1,都有f(x)﹣k(x﹣1)>0(k∈Z)恒成立,求k的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】居民消费价格指数,简称CPI,是一个反映居民消费价格水平变动情况的宏观经济指标.某年的![]() ,以下是
,以下是![]() 年居民消费价格指数的柱形图.
年居民消费价格指数的柱形图.
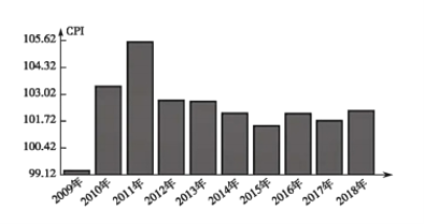
从图中可知下列说法正确的是( )
A.![]() 年居民消费价格总体呈增长趋势
年居民消费价格总体呈增长趋势
B.这十年中有些年份居民消费价格增长率超过3%
C.2009年的居民消费价格出现负增长
D.2011年的居民消费价格最高
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com