
【题目】已知等比数列![]() 的前
的前![]() 项和为
项和为![]() ,且函数
,且函数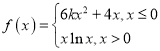 ,若方程
,若方程![]() 至少有三个实数根,则实数
至少有三个实数根,则实数![]() 的取值范围是( )
的取值范围是( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
【答案】C
【解析】
由等比数列前![]() 项和的性质,求得参数
项和的性质,求得参数![]() ,再将方程根的个数的问题,转化为函数图像交点个数的问题,利用导数求得直线与函数相切时的斜率,即可求得参数的范围.
,再将方程根的个数的问题,转化为函数图像交点个数的问题,利用导数求得直线与函数相切时的斜率,即可求得参数的范围.
因为等比数列![]() 的前
的前![]() 项和为
项和为![]()
根据等比数列前![]() 项和的性质,容易知
项和的性质,容易知![]() ,解得
,解得![]() .
.
令![]() ,则
,则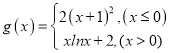
方程![]() 至少有三个实数根
至少有三个实数根
等价于![]() 至少有三个实数根,
至少有三个实数根,
也等价于函数![]() 与直线
与直线![]() 有至少三个交点,
有至少三个交点,
又![]() 是斜率为
是斜率为![]() ,且恒过
,且恒过![]() 的直线,
的直线,
故只需求出函数![]() 与直线有三个交点的临界状态时,对应直线的斜率即可.
与直线有三个交点的临界状态时,对应直线的斜率即可.
则在同一直角坐标系下画出函数图像如下所示:
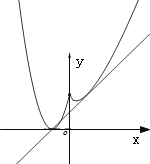
由图可知,当直线与![]() 相切时,恰有三个交点,
相切时,恰有三个交点,
设切点为![]() ,
,![]() ,故过切点的切线方程为:
,故过切点的切线方程为:
![]() ,又因为
,又因为![]() ,且该切线过点
,且该切线过点![]()
故可得![]()
即![]() ,解得
,解得![]() ,
,
故切点为![]() ,此时直线的斜率为
,此时直线的斜率为![]()
此时有三个交点,故![]() 可取;
可取;
又根据图象可知,当直线过点![]() 时,也是临界状态,
时,也是临界状态,
此时直线的斜率为![]()
此时有三个交点,故![]() 可取;
可取;
综上所述,要满足题意,只需![]() 即可.
即可.
故选:C.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源: 题型:
【题目】华为董事会决定投资开发新款软件,估计能获得![]() 万元到
万元到![]() 万元的投资收益,讨论了一个对课题组的奖励方案:奖金
万元的投资收益,讨论了一个对课题组的奖励方案:奖金![]() (单位:万元)随投资收益
(单位:万元)随投资收益![]() (单位:万元)的增加而增加,且奖金不超过
(单位:万元)的增加而增加,且奖金不超过![]() 万元,同时奖金不超过投资收益的
万元,同时奖金不超过投资收益的![]() .
.
(1)请分析函数![]() 是否符合华为要求的奖励函数模型,并说明原因;
是否符合华为要求的奖励函数模型,并说明原因;
(2)若华为公司采用模型函数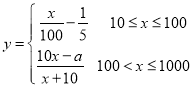 作为奖励函数模型,试确定正整数
作为奖励函数模型,试确定正整数![]() 的取值集合.
的取值集合.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆C:![]() (
(![]() )的短轴长和焦距相等,左、右焦点分别为
)的短轴长和焦距相等,左、右焦点分别为![]() 、
、![]() ,点
,点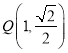 满足:
满足:![]() .已知直线l与椭圆C相交于A,B两点.
.已知直线l与椭圆C相交于A,B两点.
(1)求椭圆C的标准方程;
(2)若直线l过点![]() ,且
,且![]() ,求直线l的方程;
,求直线l的方程;
(3)若直线l与曲线![]() 相切于点
相切于点![]() (
(![]() ),且
),且![]() 中点的横坐标等于
中点的横坐标等于![]() ,证明:符合题意的点T有两个,并任求出其中一个的坐标.
,证明:符合题意的点T有两个,并任求出其中一个的坐标.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() .
.
(1)当![]() 时,求
时,求![]() 在
在![]() 处的切线方程;
处的切线方程;
(2)令![]() ,已知函数
,已知函数![]() 有两个极值点
有两个极值点![]() ,且
,且![]() ,求实数
,求实数![]() 的取值范围;
的取值范围;
(3)在(2)的条件下,若存在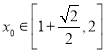 ,使不等式
,使不等式![]() 对任意
对任意![]() (取值范围内的值)恒成立,求实数
(取值范围内的值)恒成立,求实数![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在直角坐标系![]() 中,曲线
中,曲线![]() 的参数方程为
的参数方程为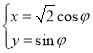 (
(![]() 为参数),以坐标原点
为参数),以坐标原点![]() 为极点,
为极点,![]() 轴的正半轴为极轴建立极坐标系,曲线
轴的正半轴为极轴建立极坐标系,曲线![]() 的极坐标方程为
的极坐标方程为![]() .
.
(1)求曲线![]() 的极坐标方程和
的极坐标方程和![]() 的直角坐标方程;
的直角坐标方程;
(2)设![]() 是曲线
是曲线![]() 上一点,此时参数
上一点,此时参数![]() ,将射线
,将射线![]() 绕原点
绕原点![]() 逆时针旋转
逆时针旋转![]() 交曲线
交曲线![]() 于点
于点![]() ,记曲线
,记曲线![]() 的上顶点为点
的上顶点为点![]() ,求
,求![]() 的面积.
的面积.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com