
【题目】已知抛物线![]() 的焦点为F,过焦点F的直线
的焦点为F,过焦点F的直线![]() 交抛物线于A,B两点,设AB的中点为M,A,B,M在准线上的射影分别为C,D,N.
交抛物线于A,B两点,设AB的中点为M,A,B,M在准线上的射影分别为C,D,N.
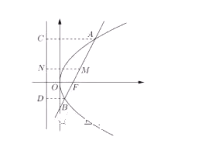
(1)求直线FN与直线AB的夹角![]() 的大小;
的大小;
(2)求证:点B,O,C三点共线.
【答案】(1)![]() (2)见解析
(2)见解析
【解析】
(1)先设A(x1,y1)、B(x2,y2)、中点M(x0,y0),利用斜率公式得出kFN![]() y0,再分类讨论:当x1=x2时,显然FN⊥AB;当x1≠x2时,证出kFNkAB=﹣1.从而知FN⊥AB成立,即可得出结论.
y0,再分类讨论:当x1=x2时,显然FN⊥AB;当x1≠x2时,证出kFNkAB=﹣1.从而知FN⊥AB成立,即可得出结论.
(2)将焦点弦AB的直线的方程代入抛物线的方程,消去x得到关于y的一元二次方程,再结合直线斜率的关系即可证得B、O、C三点共线,从而解决问题.
(1)设A(x1,y1)、B(x2,y2)、中点M(x0,y0),焦点F的坐标是(1,0).
N(﹣1,y0),∴kFN![]() y0,
y0,
当x1=x2时,显然FN⊥AB;
当x1≠x2时,kAB![]() ,
,
∴kFNkAB=﹣1.
∴FN⊥AB.综上所述知FN⊥AB成立,
即直线FN与直线AB的夹角θ的大小为90°;
(2)由x=my+1与抛物线方程联立,可得y2﹣4my﹣4=0,∴y1y2=﹣4,
∴A在准线上的射影为C,
∴C(﹣1,y1),∴kOC=﹣y1,
∵kOB![]() ,y1y2=﹣4,
,y1y2=﹣4,
∴kOB=kOC,∴点B、O、C三点共线.


 华东师大版一课一练系列答案
华东师大版一课一练系列答案科目:高中数学 来源: 题型:
【题目】惠州市某商店销售某海鲜,经理统计了春节前后50天该海鲜的日需求量![]() (
(![]() ,单位:公斤),其频率分布直方图如下图所示.该海鲜每天进货1次,每销售1公斤可获利40元;若供大于求,剩余的海鲜削价处理,削价处理的海鲜每公斤亏损10元;若供不应求,可从其它商店调拨,调拨的海鲜销售1公斤可获利30元.假设商店该海鲜每天的进货量为14公斤,商店销售该海鲜的日利润为
,单位:公斤),其频率分布直方图如下图所示.该海鲜每天进货1次,每销售1公斤可获利40元;若供大于求,剩余的海鲜削价处理,削价处理的海鲜每公斤亏损10元;若供不应求,可从其它商店调拨,调拨的海鲜销售1公斤可获利30元.假设商店该海鲜每天的进货量为14公斤,商店销售该海鲜的日利润为![]() 元.
元.
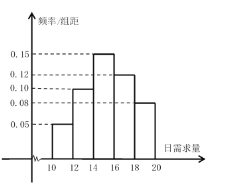
(1)求商店日利润![]() 关于日需求量
关于日需求量![]() 的函数表达式.
的函数表达式.
(2)根据频率分布直方图,
①估计这50天此商店该海鲜日需求量的平均数.
②假设用事件发生的频率估计概率,请估计日利润不少于620元的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某地区2020年清明节前后3天每天下雨的概率为60%,通过模拟实验的方法来计算该地区这3天中恰好有2天下雨的概率:用随机数![]() (
(![]() ,且
,且![]() )表示是否下雨:当
)表示是否下雨:当![]() 时表示该地区下雨,当
时表示该地区下雨,当![]() 时,表示该地区不下雨,从随机数表中随机取得20组数如下
时,表示该地区不下雨,从随机数表中随机取得20组数如下
332 714 740 945 593 468 491 272 073 445
992 772 951 431 169 332 435 027 898 719
(1)求出![]() 的值,并根据上述数表求出该地区清明节前后3天中恰好有2天下雨的概率;
的值,并根据上述数表求出该地区清明节前后3天中恰好有2天下雨的概率;
(2)从2011年开始到2019年该地区清明节当天降雨量(单位:![]() )如下表:(其中降雨量为0表示没有下雨).
)如下表:(其中降雨量为0表示没有下雨).
时间 | 2011年 | 2012年 | 2013年 | 2014年 | 2015年 | 2016年 | 2017年 | 2018年 | 2019年 |
年份 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 |
降雨量 | 29 | 28 | 26 | 27 | 25 | 23 | 24 | 22 | 21 |
经研究表明:从2011年开始至2020年, 该地区清明节有降雨的年份的降雨量![]() 与年份
与年份![]() 成线性回归,求回归直线
成线性回归,求回归直线![]() ,并计算如果该地区2020年(
,并计算如果该地区2020年(![]() )清明节有降雨的话,降雨量为多少?(精确到0.01)
)清明节有降雨的话,降雨量为多少?(精确到0.01)
参考公式: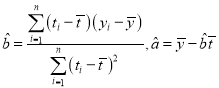 .
.
参考数据:![]() ,
,![]() ,
,
![]() ,
,![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某公司为了预测下月产品销售情况,找出了近7个月的产品销售量![]() (单位:万件)的统计表:
(单位:万件)的统计表:
月份代码 | 1 | 2 | 3 | 4 | 5 | 6 | 7 |
销售量 |
|
|
|
|
|
|
|
但其中数据污损不清,经查证![]() ,
,![]() ,
, .
.
(1)请用相关系数说明销售量![]() 与月份代码
与月份代码![]() 有很强的线性相关关系;
有很强的线性相关关系;
(2)求![]() 关于
关于![]() 的回归方程(系数精确到0.01);
的回归方程(系数精确到0.01);
(3)公司经营期间的广告宣传费![]() (单位:万元)(
(单位:万元)(![]() ),每件产品的销售价为10元,预测第8个月的毛利润能否突破15万元,请说明理由.(毛利润等于销售金额减去广告宣传费)
),每件产品的销售价为10元,预测第8个月的毛利润能否突破15万元,请说明理由.(毛利润等于销售金额减去广告宣传费)
参考公式及数据:![]() ,相关系数
,相关系数 ,当
,当![]() 时认为两个变量有很强的线性相关关系,回归方程
时认为两个变量有很强的线性相关关系,回归方程![]() 中斜率和截距的最小二乘估计公式分别为
中斜率和截距的最小二乘估计公式分别为 ,
,![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() ,
,![]() 、
、![]() 为椭圆的左、右焦点,
为椭圆的左、右焦点,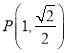 为椭圆上一点,且
为椭圆上一点,且![]() .
.
(1)求椭圆的标准方程;
(2)设直线![]() ,过点
,过点![]() 的直线交椭圆于
的直线交椭圆于![]() 、
、![]() 两点,线段
两点,线段![]() 的垂直平分线分别交直线
的垂直平分线分别交直线![]() 、直线
、直线![]() 于
于![]() 、
、![]() 两点,当
两点,当![]() 最小时,求直线
最小时,求直线![]() 的方程.
的方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某公司要在一条笔直的道路边安装路灯,要求灯柱AB与底面垂直,灯杆BC与灯柱AB所在的平面与道路走向垂直,路灯C采用锥形灯罩,射出的管线与平面ABC部分截面如图中阴影所示,![]() 路宽AD=24米,设
路宽AD=24米,设![]()

(1)求灯柱AB的高h(用![]() 表示);
表示);
(2)此公司应该如何设置![]() 的值才能使制作路灯灯柱AB和灯杆BC所用材料的总长度最小?最小值为多少?
的值才能使制作路灯灯柱AB和灯杆BC所用材料的总长度最小?最小值为多少?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知曲线![]() ,
,![]() 相邻对称轴之间的距离为
相邻对称轴之间的距离为![]() ,且函数
,且函数![]() 在
在![]() 处取得最大值,则下列命题正确的个数为( )
处取得最大值,则下列命题正确的个数为( )
①当![]() 时,m的取值范围是
时,m的取值范围是 ;②将
;②将![]() 的图象向左平移
的图象向左平移![]() 个单位后所对应的函数为偶函数;③函数
个单位后所对应的函数为偶函数;③函数![]() 的最小正周期为
的最小正周期为![]() ;④函数
;④函数![]() 在区间
在区间![]() 上有且仅有一个零点.
上有且仅有一个零点.
A.1B.2C.3D.4
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com