
【题目】在直角坐标系![]() 中,曲线
中,曲线![]() :
:![]() (
(![]() 为参数),曲线
为参数),曲线![]() :
: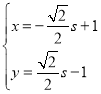 (
(![]() 为参数),以O为极点,
为参数),以O为极点,![]() 轴的非负半轴为极轴的极坐标系中,已知曲线
轴的非负半轴为极轴的极坐标系中,已知曲线![]() 的极坐标方程为
的极坐标方程为![]() ,记曲线
,记曲线![]() 与
与![]() 的交点为
的交点为![]() .
.
(1)求点![]() 的极坐标;
的极坐标;
(2)设曲线![]() 与
与![]() 相交于A,B两点,求
相交于A,B两点,求![]() 的值.
的值.
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源: 题型:
【题目】某快递公司收取快递费用的标准是:重量不超过![]() 的包裹收费10元;重量超过
的包裹收费10元;重量超过![]() 的包裹,除收费10元之外,超过
的包裹,除收费10元之外,超过![]() 的部分,每超出
的部分,每超出![]() (不足
(不足![]() ,按
,按![]() 计算)需要再收费5元.该公司近60天每天揽件数量的频率分布直方图如下图所示(同一组数据用该区间的中点值作代表).
计算)需要再收费5元.该公司近60天每天揽件数量的频率分布直方图如下图所示(同一组数据用该区间的中点值作代表).
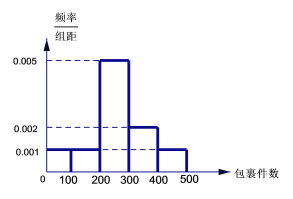
(1)求这60天每天包裹数量的平均值和中位数;
(2)该公司从收取的每件快递的费用中抽取5元作为前台工作人员的工资和公司利润,剩余的作为其他费用.已知公司前台有工作人员3人,每人每天工资100元,以样本估计总体,试估计该公司每天的利润有多少元?
(3)小明打算将![]() 四件礼物随机分成两个包裹寄出,且每个包裹重量都不超过
四件礼物随机分成两个包裹寄出,且每个包裹重量都不超过![]() ,求他支付的快递费为45元的概率.
,求他支付的快递费为45元的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,已知平行四边形![]() 中,
中,![]() ,
,![]() ,
,![]() 为边
为边![]() 的中点,将
的中点,将![]() 沿直线
沿直线![]() 翻折成
翻折成![]() .若
.若![]() 为线段
为线段![]() 的中点,则在
的中点,则在![]() 翻折过程中,有下列三个命题:
翻折过程中,有下列三个命题:
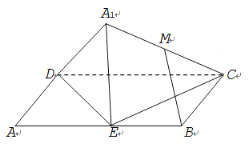
①线段![]() 的长是定值;
的长是定值;
②存在某个位置,使![]() ;
;
③存在某个位置,使![]() 平面
平面![]() .
.
其中正确的命题有______. (填写所有正确命题的编号)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】学校艺术节对![]() 四件参赛作品只评一件一等奖,在评奖揭晓前,甲,乙,丙,丁四位同学对这四件参赛作品预测如下:
四件参赛作品只评一件一等奖,在评奖揭晓前,甲,乙,丙,丁四位同学对这四件参赛作品预测如下:
甲说:“是![]() 或
或![]() 作品获得一等奖”; 乙说:“
作品获得一等奖”; 乙说:“ ![]() 作品获得一等奖”;
作品获得一等奖”;
丙说:“ ![]() 两件作品未获得一等奖”; 丁说:“是
两件作品未获得一等奖”; 丁说:“是![]() 作品获得一等奖”.
作品获得一等奖”.
评奖揭晓后,发现这四位同学中只有两位说的话是对的,则获得一等奖的作品是_________.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】斐波那契数列0,1,1,2,3,5,8,13,…,是意大利数学家列昂纳多·斐波那契发明的,定义如下:![]() ,
,![]() ,
,![]() .某同学设计了一个求解斐波那契数列前
.某同学设计了一个求解斐波那契数列前![]() 项和的程序框图,如图所示,若输出
项和的程序框图,如图所示,若输出![]() 的值为232,则处理框和判断框中应该分别填入( )
的值为232,则处理框和判断框中应该分别填入( )

A.![]() ,
,![]() B.
B.![]() ,
,![]()
C.![]() ,
,![]() D.
D.![]() ,
,![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com