
【题目】已知函数f(x)=![]() .
.
(1)求f(2)+f![]() ,f(3)+f
,f(3)+f![]() 的值;
的值;
(2)求证:f(x)+f![]() 是定值;
是定值;
(3)求f(2)+f![]() +f(3)+f
+f(3)+f![]() +…+
+…+![]() +f
+f![]() 的值.
的值.
科目:高中数学 来源: 题型:
【题目】对于数列{an},若an+2﹣an=d(d是与n无关的常数,n∈N*),则称数列{an}叫做“弱等差数列”,已知数列{an}满足:a1=t,a2=s且an+an+1=an+b对于n∈N*恒成立,(其中t,s,a,b都是常数).
(1)求证:数列{an}是“弱等差数列”,并求出数列{an}的通项公式;
(2)当t=1,s=3时,若数列{an}是等差数列,求出a、b的值,并求出{an}的前n项和Sn;
(3)若s>t,且数列{an}是单调递增数列,求a的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
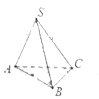
【题目】如图:在三棱锥![]() 中,已知底面
中,已知底面![]() 是以
是以![]() 为斜边的等腰直角三角形,且侧棱长
为斜边的等腰直角三角形,且侧棱长![]() ,则三棱锥
,则三棱锥![]() 的外接球的表面积等于__________.
的外接球的表面积等于__________.
【答案】![]()
【解析】三棱锥![]() 的外接球的球心在SM上(M为AB 中点),球半径设为R,则
的外接球的球心在SM上(M为AB 中点),球半径设为R,则![]()
点睛:涉及球与棱柱、棱锥的切、接问题时,一般过球心及多面体中的特殊点(一般为接、切点)或线作截面,把空间问题转化为平面问题,再利用平面几何知识寻找几何体中元素间的关系,或只画内切、外接的几何体的直观图,确定球心的位置,弄清球的半径(直径)与该几何体已知量的关系,列方程(组)求解.
【题型】填空题
【结束】
16
【题目】已知斜率![]() 的直线
的直线![]() 过抛物线
过抛物线![]() 的焦点,且与抛物线相交于
的焦点,且与抛物线相交于![]() 、
、![]() 两点,分别过点
两点,分别过点![]() 、
、![]() 若作抛物线的两条切线相交于点
若作抛物线的两条切线相交于点![]() ,则
,则![]() 的面积为__________.
的面积为__________.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知f(x)= ![]() sin2x﹣cos2x﹣
sin2x﹣cos2x﹣ ![]() ,(x∈R).
,(x∈R).
(1)求函数f(x)的最小值和最小正周期;
(2)设△ABC的内角A、B、C的对边分别为a、b、c,且c= ![]() ,f(C)=0,若
,f(C)=0,若 ![]() =(1,sinA)与
=(1,sinA)与 ![]() =(2,sinB)共线,求a,b的值.
=(2,sinB)共线,求a,b的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】给出下列四个命题:
1)若α>β且α、β都是第一象限角,则tanα>tanβ;
2)“对任意x∈R,都有x2≥0”的否定为“存在x0∈R,使得 ![]() <0”;
<0”;
3)已知命题p:所有有理数都是实数,命题q:正数的对数都是负数,则(p)∨q为真命题;
4)函数 ![]() 是偶函数.
是偶函数.
其中真命题的个数是( )
A.1
B.2
C.3
D.4
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某城镇社区为了丰富辖区内广大居民的业余文化生活,创建了社区“文化丹青”大型活动场所,配备了各种文化娱乐活动所需要的设施,让广大居民健康生活、积极向上,社区最近四年内在“文化丹青”上的投资金额统计数据如表: (为了便于计算,把2015年简记为5,其余以此类推)
年份 | 5 | 6 | 7 | 8 |
投资金额 | 15 | 17 | 21 | 27 |
(Ⅰ)利用所给数据,求出投资金额![]() 与年份
与年份![]() 之间的回归直线方程
之间的回归直线方程![]() ;
;
(Ⅱ) 预测该社区在2019年在“文化丹青”上的投资金额.
附:对于一组数据![]() , 其回归直线
, 其回归直线![]() 的斜率和截距的最小二乘估计分别为
的斜率和截距的最小二乘估计分别为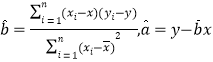 .
.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com