练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    解答题

    已知tanα＝3tanβ，其中α、β为锐角，求u＝α＝β的最大值．

    答案：
    解析：

    　　解：∵α、β为锐角，且tanα＝3tanβ，∴α＞β．

    　　∴0＜α－β＜．

    　　又tanβ＞0，且tanu＝tan(α－β)＝＝

    　　＝＝≤＝．

    　　当且仅当＝3tanβ，即tanβ＝，亦即β＝时取等号．

    　　又∵正切函数在(0，)内单调递增，

    　　∴u＝α－β≤．

    　　故u的最大值为，此时α＝，β＝．


    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源：2004年高考教材全程总复习试卷·数学 题型：038

    已知tanα＝3，求值：

    (1)．

    (2)2sin2α－3sinαcosα．

    查看答案和解析>>

    科目：高中数学 来源：成功之路·突破重点线·数学（学生用书） 题型：044

    已知tan(3π－α)＝a2，且|cos(π－α)|＝－cosα，求cosα的值．

    查看答案和解析>>

    科目：高中数学 来源：成功之路·突破重点线·数学（学生用书） 题型：044

    已知cosα－sinα＝，且π＜α＜π，

    求sinα和tan(α＋)的值．

    查看答案和解析>>

    科目：高中数学 来源：2004年高考教材全程总复习试卷·数学 题型：044

    已知函数f(x)＝2acos2x＋bsinxcosx且f(0)＝2，f()＝＋．

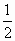    (1)求使f(x)＞2的x的集合．

    (2)若α－β≠kπ(k∈Z)且f(α)＝f(β)，求tan(α＋β)的值．

    查看答案和解析>>

    同步练习册答案