
分析 根据题意可得{an}是由一个首项为正数,公差为负数的等差数列,{an}的各项取绝对值后得到一个新数列{bn},求出它的前10项和即可,应转化为求数列{an}的和.
解答 解:∵数列{an}的前n项和为Sn=10n-n2,
∴Sn-1=10(n-1)-(n-1)2,(n≥2)
两式相减得an=11-2n,
又n=1时,a1=S1=10-1=9,满足上式;
∴an=11-2n,
∴bn=|an|=|11-2n|;
显然n≤5时,bn=an=11-2n,Tn=10n-n2;
n≥6时,bn=-an=2n-11,
∴Tn=(a1+a2+…+a5)-(a6+a7+…+an)=2S5-Sn=50-10n+n2
故Tn=$\left\{\begin{array}{l}{10n{-n}^{2},n≤5}\\{{n}^{2}-10n+50,n≥6}\end{array}\right.$
∴数列{bn}的前10项和为:T10=102-10×10+50=50.
故答案为:50.
点评 本题主要考查了数列的通项与求和方法的运用问题,也考查了分析问题与解答问题的能力,是中档题目.


科目:高中数学 来源: 题型:选择题
| A. | 455 068 047 447 176 | B. | 169 105 071 286 443 | ||
| C. | 050 358 074 439 332 | D. | 447 176 335 025 212 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{\sqrt{3}}{2}$ | B. | $\frac{1}{2}$ | C. | -$\frac{1}{2}$ | D. | -$\frac{\sqrt{3}}{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | P+R=2Q | B. | Q(Q-P)=P(R-P) | C. | Q(Q-P)=R | D. | Q2=PR |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $a<\frac{1}{3}$ | B. | $a≤\frac{1}{3}$ | C. | $\frac{1}{6}≤a<\frac{1}{3}$ | D. | $0<a<\frac{1}{3}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | -$\frac{3}{2}$ | B. | -$\frac{1}{2}$ | C. | $\frac{1}{2}$ | D. | $\frac{3}{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
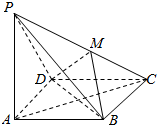 如图,在四棱锥P-ABCD中,PA⊥底面ABCD,且底面ABCD是正方形,DM⊥PC,垂足为M.
如图,在四棱锥P-ABCD中,PA⊥底面ABCD,且底面ABCD是正方形,DM⊥PC,垂足为M.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com