
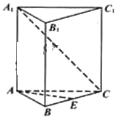
【题目】如图,已知正三棱柱ABC=A1B1C1的各棱长都是4,E是BC的中点,动点F在侧棱CC1上,且不与点C重合.
(1)当CF=1时,求证:EF⊥A1C;
(2)设二面角C﹣AF﹣E的大小为θ,求tanθ的最小值.
【答案】(1)见解析 (2)![]()
【解析】
(1)过E作EN⊥AC于N,连接EF,NF,AC1,由直棱柱的性质可知,底面ABC⊥侧面A1C
∴EN⊥侧面A1C
NF为EF在侧面A1C内的射影
在直角三角形CNF中,CN=1
则由![]() ,得NF∥AC1,又AC1⊥A1C,故NF⊥A1C
,得NF∥AC1,又AC1⊥A1C,故NF⊥A1C
由三垂线定理可知EF⊥A1C
(2)连接AF,过N作NM⊥AF与M,连接ME
由(1)可知EN⊥侧面A1C,根据三垂线定理得EM⊥AF
∴∠EMN是二面角C﹣AF﹣E的平面角即∠EMN=θ
设∠FAC=α则0°<α≤45°,
在直角三角形CNE中,NE=![]() ,在直角三角形AMN中,MN=3sinα
,在直角三角形AMN中,MN=3sinα
故tanθ=![]() ,又0°<α≤45°∴0<sinα≤
,又0°<α≤45°∴0<sinα≤![]()
故当α=45°时,tanθ达到最小值,
tanθ=![]() ,此时F与C1重合
,此时F与C1重合


 黄冈小状元解决问题天天练系列答案
黄冈小状元解决问题天天练系列答案 三点一测快乐周计划系列答案
三点一测快乐周计划系列答案科目:高中数学 来源: 题型:
【题目】在平面直角坐标系中,以原点为极点,![]() 轴为极轴建立极坐标系,曲线
轴为极轴建立极坐标系,曲线![]() 的方程为
的方程为![]() (
(![]() 为参数),曲线
为参数),曲线![]() 的极坐标方程为
的极坐标方程为![]() ,若曲线
,若曲线![]() 与
与![]() 相交于
相交于![]() 、
、![]() 两点.
两点.
(1)求![]() 的值;
的值;
(2)求点![]() 到
到![]() 、
、![]() 两点的距离之积.
两点的距离之积.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在抽取彩票“双色球”中奖号码时,有33个红色球,每个球的编号分别为01,02,…,33.一位彩民用随机数表法选取6个号码作为6个红色球的编号,选取方法是从下面的随机数表中第1行第6列的数字3开始,从左向右读数,则依次选出的第3个红色球的编号为( )
49 54 43 54 82 17 37 93 23 78 87 35 20 96 43 84 26 34 91 64 |
57 24 55 06 88 77 04 74 47 67 21 76 33 50 25 83 92 12 06 76 |
A.21B.32C.09D.20
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() 的中心在坐标原点,焦点在
的中心在坐标原点,焦点在![]() 轴上,离心率为
轴上,离心率为![]() ,椭圆
,椭圆![]() 上的点到焦点距离的最大值为
上的点到焦点距离的最大值为![]() .
.
(1)求椭圆![]() 的标准方程;
的标准方程;
(2)斜率为![]() 的直线
的直线![]() 与椭圆
与椭圆![]() 交于不同的两点
交于不同的两点![]() ,且线段
,且线段![]() 的中垂线交
的中垂线交![]() 轴于点
轴于点![]() ,求点
,求点![]() 横坐标的取值范围.
横坐标的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】为迎接2022年北京冬季奥运会,普及冬奥知识,某校开展了“冰雪答题王”冬奥知识竞赛活动.现从参加冬奥知识竞赛活动的学生中随机抽取了100名学生,将他们的比赛成绩(满分为100分)分为6组:![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,得到如图所示的频率分布直方图.
,得到如图所示的频率分布直方图.
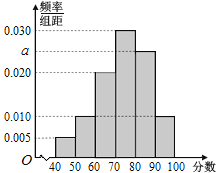
(1)求![]() 的值;
的值;
(2)估计这100名学生的平均成绩(同一组中的数据用该组区间的中点值为代表);
(3)在抽取的100名学生中,规定:比赛成绩不低于80分为“优秀”,比赛成绩低于80分为“非优秀”.请将下面的2×2列联表补充完整,并判断是否有99.9%的把握认为“比赛成绩是否优秀与性别有关”?
优秀 | 非优秀 | 合计 | |
男生 | 40 | ||
女生 | 50 | ||
合计 | 100 |
参考公式及数据:![]()
| 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】今年入冬以来,我市天气反复.在下图中统计了我市上个月前15天的气温,以及相对去年同期的气温差(今年气温-去年气温,单位:摄氏度),以下判断错误的是( )
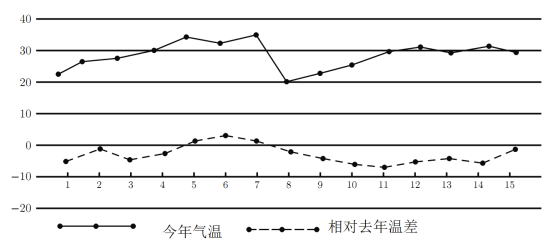
A.今年每天气温都比去年气温低B.今年的气温的平均值比去年低
C.今年8-12号气温持续上升D.今年8号气温最低
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知平面直角坐标系![]() ,直线
,直线![]() 过点
过点![]() ,且倾斜角为
,且倾斜角为![]() ,以
,以![]() 为极点,
为极点,![]() 轴的非负半轴为极轴建立极坐标系,圆
轴的非负半轴为极轴建立极坐标系,圆![]() 的极坐标方程为
的极坐标方程为![]() .
.
(1)求直线![]() 的参数方程和圆
的参数方程和圆![]() 的标准方程;
的标准方程;
(2)设直线![]() 与圆
与圆![]() 交于
交于![]() 、
、![]() 两点,若
两点,若![]() ,求直线
,求直线![]() 的倾斜角的
的倾斜角的![]() 值.
值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com