解:(1)令x=y=1,得f(1)=0;令
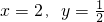
,得
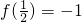
(2分)
y=f(x)在(0,+∞)上单调递增.下面证明:
任取0<x
1<x
2,则

,
∵当x>1时,f(x)>0,∴
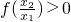
在已知式中令
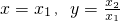
,得
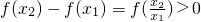
,即证.(4分)
(2)当n≥2时,∵f(S
n)=f(a
n)+f(a
n+1)-1
∴f(S
n)+1=f(a
n)+f(a
n+1),即f(2S
n)=f(a
n(a
n+1))
∵y=f(x)在(0,+∞)上单调递增,
∴2S
n=a
n(a
n+1)(6分)
∴2S
n+1=a
n+1(a
n+1+1)
两式相减得:
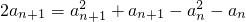
,即(a
n+1+a
n)(a
n+1-a
n-1)=0∵a
n>0,
∴a
n+1-a
n=1∴数列{a
n}从第二项起,是以1为公差的等差数列…(7分)
又在2S
n=a
n(a
n+1)中令n=2可得:a
2=3
综上,
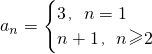
.(8分)
(3)n=1时,
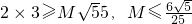
(9分)
n≥2时,
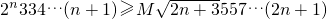
∴
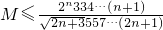
令
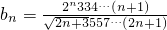
,
则
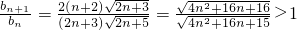
∴{b
n}是递增数列
∴
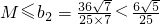
∴
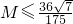
(12分)
分析:(1)利用赋值法可求函数值,利用单调性的定义证明函数的单调性;
(2)确定数列通项与和的关系,再写一式,两式相减,即可求得数列的通项;
(3)利用分离参数法,求出函数的最值,即可求得M的范围.
点评:本题考查抽象函数的单调性,考查数列的通项,考查恒成立问题,解题的关键是分离参数,求函数的最值.

 的值,试判断y=f(x)在(0,+∞)上的单调性,并加以证明;
的值,试判断y=f(x)在(0,+∞)上的单调性,并加以证明;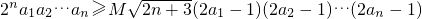 对于一切正整数n均成立?若存在,求出M的范围;若不存在,请说明理由.
对于一切正整数n均成立?若存在,求出M的范围;若不存在,请说明理由.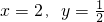 ,得
,得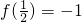 (2分)
(2分) ,
,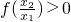
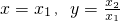 ,得
,得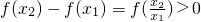 ,即证.(4分)
,即证.(4分)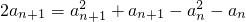 ,即(an+1+an)(an+1-an-1)=0∵an>0,
,即(an+1+an)(an+1-an-1)=0∵an>0,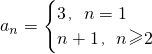 .(8分)
.(8分)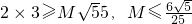 (9分)
(9分)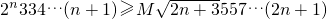
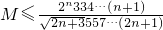
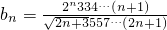 ,
,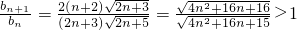
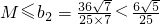
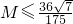 (12分)
(12分)

 举一反三单元同步过关卷系列答案
举一反三单元同步过关卷系列答案