
【题目】已知椭圆![]() 的离心率为
的离心率为![]() ,且过点
,且过点 .
.
(1)求![]() 的方程;
的方程;
(2)是否存在直线![]() 与
与![]() 相交于
相交于![]() 两点,且满足:①
两点,且满足:①![]() 与
与![]() (
(![]() 为坐标原点)的斜率之和为2;②直线
为坐标原点)的斜率之和为2;②直线![]() 与圆
与圆![]() 相切,若存在,求出
相切,若存在,求出![]() 的方程;若不存在,请说明理由.
的方程;若不存在,请说明理由.
 高中必刷题系列答案
高中必刷题系列答案科目:高中数学 来源: 题型:
【题目】选修4-4:坐标系与参数方程
已知极坐标系的极点为直角坐标系![]() 的原点,极轴为
的原点,极轴为![]() 轴的正半轴,两种坐标系中的长度单位相同,圆
轴的正半轴,两种坐标系中的长度单位相同,圆![]() 的直角坐标方程为
的直角坐标方程为![]() ,直线
,直线![]() 的参数方程为
的参数方程为![]() (
(![]() 为参数),射线
为参数),射线![]() 的极坐标方程为
的极坐标方程为![]() .
.
(1)求圆![]() 和直线
和直线![]() 的极坐标方程;
的极坐标方程;
(2)已知射线![]() 与圆
与圆![]() 的交点为
的交点为![]() ,与直线
,与直线![]() 的交点为
的交点为![]() ,求线段
,求线段![]() 的长.
的长.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】利用简单随机抽样从某小区抽取100户居民进行月用电量调查,发现其用电量都在50到350度之间,频率分布直方图如图所示.在这些用户中,用电量落在区间[150,250]内的户数为( ) 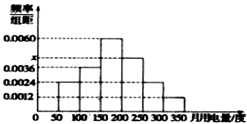
A.46
B.48
C.50
D.52
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某市医疗保险实行定点医疗制度,按照“就近就医、方便管理”的原则,参加保险人员可自主选择四家医疗保险定点医院和一家社区医院作为本人就诊的医疗机构.若甲、乙、丙、丁4名参加保险人员所在地区附近有A,B,C三家社区医院,并且他们的选择是相互独立的.
(Ⅰ)求甲、乙两人都选择A社区医院的概率;
(Ⅱ)求甲、乙两人不选择同一家社区医院的概率;
(Ⅲ)设4名参加保险人员中选择A社区医院的人数为ξ,求ξ的分布列和数学期望.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】选修4-4:参数方程与极坐标系
在平面直角坐标系![]() 中,直线
中,直线![]() 的参数方程为
的参数方程为![]() (
(![]() 为参数,
为参数, ![]() 为倾斜角),以坐标原点O为极点,
为倾斜角),以坐标原点O为极点, ![]() 轴的正半轴为极轴的极坐标系中,曲线
轴的正半轴为极轴的极坐标系中,曲线![]() 的极坐标方程为
的极坐标方程为![]()
(1)求曲线![]() 的直角坐标方程,并 求C的焦点F的直角坐标;
的直角坐标方程,并 求C的焦点F的直角坐标;
(2)已知点![]() ,若直线
,若直线![]() 与C相交于A,B两点,且
与C相交于A,B两点,且![]() ,求
,求![]() 的面积.
的面积.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在四棱锥P﹣ABCD中,PA⊥平面ABCD,AD∥BC,BC=2AD,PB⊥AC,Q是线段PB的中点. (Ⅰ)求证:AB⊥平面PAC;
(Ⅱ)求证:AQ∥平面PCD.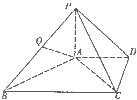
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com