
【题目】点![]() 、
、![]() 、
、![]() 分别是正方体
分别是正方体![]() 的棱
的棱![]() ,
,![]() ,
,![]() 的中点,则下列命题中的真命题是__________(写出所有真命题的序号).
的中点,则下列命题中的真命题是__________(写出所有真命题的序号).
①以正方体的顶点为顶点的三棱锥的四个面中最多可以四个面都是直角三角形;
②点![]() 在直线
在直线![]() 上运动时,总有
上运动时,总有![]() ;
;
③点![]() 在直线
在直线![]() 上运动时,三棱锥
上运动时,三棱锥![]() 的体积是定值;
的体积是定值;
④若![]() 是正方体的面
是正方体的面![]() ,(含边界)内一动点,且点
,(含边界)内一动点,且点![]() 到点
到点![]() 和
和![]() 的距离相等,则点
的距离相等,则点![]() 的轨迹是一条线段.
的轨迹是一条线段.
【答案】①②④
【解析】
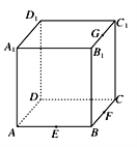
根据题意画出正方体![]() .
.
根据图像可知![]() 四个面都是直角三角形,①对;根据图象易证
四个面都是直角三角形,①对;根据图象易证![]() 面
面![]() ,所以不论点
,所以不论点![]() 在直线
在直线![]() 上如何运动,总有
上如何运动,总有![]() ,②对;根据等体积关系有
,②对;根据等体积关系有![]() ,面
,面![]() 不变,但高在变,所以三棱锥
不变,但高在变,所以三棱锥![]() 的体积不是定值,③错;
的体积不是定值,③错;
④以![]() 为
为![]() 轴,以
轴,以![]() 为
为![]() 轴建平面直角坐标系,设
轴建平面直角坐标系,设![]() ,棱长为1.根据距离公式可得
,棱长为1.根据距离公式可得![]() ,
,![]() .且
.且![]() ,
, ![]() 的轨迹是线段
的轨迹是线段![]() .④对.
.④对.
解:画出正方体![]() .
.
①四面体及![]() 四个面都是直角三角形,①对;
四个面都是直角三角形,①对;
②在平面![]() 中有
中有![]() ,又正方体中
,又正方体中![]() ,从而可以得到
,从而可以得到![]() 面
面![]() ,所以不论点
,所以不论点![]() 在直线
在直线![]() 上如何运动,总有
上如何运动,总有![]() ,②对;
,②对;
③因为![]() ,面
,面![]() 不变,底面面积不变,点
不变,底面面积不变,点![]() 在直线
在直线![]() 上运动时,点
上运动时,点![]() 到平面
到平面![]() 的距离在变,即高在变,所以三棱锥
的距离在变,即高在变,所以三棱锥![]() 的体积不是定值,③错;
的体积不是定值,③错;
④以![]() 为
为![]() 轴,以
轴,以![]() 为
为![]() 轴在平面
轴在平面![]() 所在平面建平面直角坐标系,设
所在平面建平面直角坐标系,设![]() ,棱长为1.则
,棱长为1.则![]()
![]() ,
,![]()
![]() .因为
.因为![]() ,所以
,所以![]() ,即
,即![]() 的轨迹是线段
的轨迹是线段![]() .④对.
.④对.
故答案为: ①②④


科目:高中数学 来源: 题型:
【题目】武汉市政府为了给“世界军运会”营造良好交通环境,特招聘了一批交通协管员,这些协管员的年龄都在![]() 之间,按年龄情况对他们进行统计得到的频率分布直方图如下,其中年龄在
之间,按年龄情况对他们进行统计得到的频率分布直方图如下,其中年龄在![]() 岁的有10人,
岁的有10人,![]() 岁的有45人.
岁的有45人.
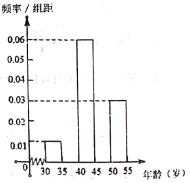
(1)补全频率分布直方图,并估计协管员的年龄中位数;
(2)为感谢年长的协管员的支持,利用分层抽样的方法从年龄在![]() 的协管员中抽取5人,并从这5人中再抽取3人,各赠送一份礼品,求仅有一人年龄在
的协管员中抽取5人,并从这5人中再抽取3人,各赠送一份礼品,求仅有一人年龄在![]() 的概率.
的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如下图,汉诺塔问题是指有3根杆子A,B,C.B杆上有若干碟子,把所有碟子从B杆移到A杆上,每次只能移动一个碟子,大的碟子不能叠在小的碟子上面.把B杆上的4个碟子全部移到A杆上,最少需要移动( )次. ( )
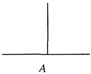
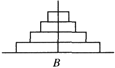
A.12 B.15 C.17 D.19
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】2019年12月,全国各中小学全体学生都参与了《禁毒知识》的答题竞赛,现从某校高一年级参加考试的学生中抽出60名学生,将其成绩(单位:分)整理后,得到如下频率分布直方图(其中分组区间为![]() ,
,![]() ,…
,…![]() ).
).
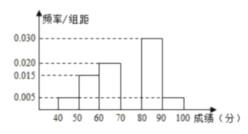
(1)求成绩在![]() 的频率,并补全此频率分布直方图;
的频率,并补全此频率分布直方图;
(2)求这次考试成绩的中位数的估计值;
(3)若从抽出的成绩在![]() 和
和![]() 的学生中任选两人,求他们的成绩在同一分组区间的概率.
的学生中任选两人,求他们的成绩在同一分组区间的概率.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com