
【题目】给出下列说法:①球的半径是球面上任意一点与球心的连线;②球的直径是球面上任意两点的连线;③用一个平面截一个球面,得到的是一个圆;④球常用表示球心的字母表示.
其中说法正确的是______.
科目:高中数学 来源: 题型:
【题目】“根据《中华人民共和国道路交通安全法》规定:车辆驾驶员血液酒精浓度在20~80 mg/100ml(不含80)之间,属于酒后驾车,血液酒精浓度在80mg/100ml(含80)以上时,属醉酒驾车.”某市交警在该市一交通岗前设点对过往的车辆进行抽查,经过一晚的抽查,共查出酒后驾车者60名,图甲是用酒精测试仪对这60 名酒后驾车者血液中酒精浓度进行检测后依所得结果画出的频率分布直方图.
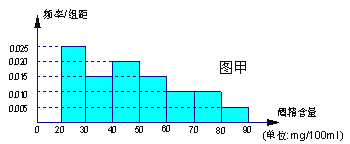
(1)统计方法中,同一组数据常用该组区间的中点值作为代表,图乙的程序框图是对这60名酒后驾车者血液的酒精浓度做进一步的统计,求出图乙输出的S的值,并说明S的统计意义;(图乙中数据![]() 与
与![]() 分别表示图甲中各组的组中值及频率)
分别表示图甲中各组的组中值及频率)

(2)本次行动中,吴、李两位先生都被酒精测试仪测得酒精浓度属于70~90![]() 的范围,但他俩坚称没喝那么多,是测试仪不准,交警大队队长决定在被酒精测试仪测得酒精浓度属于70~90
的范围,但他俩坚称没喝那么多,是测试仪不准,交警大队队长决定在被酒精测试仪测得酒精浓度属于70~90![]() 范围的酒后驾车者中随机抽出2人抽血检验,设
范围的酒后驾车者中随机抽出2人抽血检验,设![]() 为吴、李两位先生被抽中的人数,求
为吴、李两位先生被抽中的人数,求![]() 的分布列,并求吴、李两位先生至少有1人被抽中的概率.
的分布列,并求吴、李两位先生至少有1人被抽中的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】宜昌一中江南新校区拟建一个扇环形状的花坛(如图所示),按设计要求扇环的周长为30米,其中大圆弧所在圆的半径为10米,设小圆弧所在圆的半径为![]() 米,圆心角
米,圆心角![]() (弧度).
(弧度).
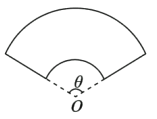
(1)求![]() 关于
关于![]() 的函数关系式;
的函数关系式;
(2)已知对花坛的边缘(实线部分)进行装饰时,直线部分的装饰费用为4元/米,弧线部分的装饰费用为9元/米,设花坛的面积与装饰总费用之比为![]() ,求
,求![]() 关于
关于![]() 的函数关系式,并求出
的函数关系式,并求出![]() 的最大值.
的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某市组织500名志愿者参加敬老活动,为方便安排任务将所有志愿者按年龄(单位:岁)分组,得到的频率分布表如下.现要从年龄较小的第1,2,3组中用分层抽样的方法抽取6人担任联系人.
年龄(岁) | 频率 | |
第1组 |
| 0.1 |
第2组 |
| 0.1 |
第3组 |
| 0.4 |
第4组 |
| 0.3 |
第5组 |
| 0.1 |
(1)应分别在第1,2,3组中抽取志愿者多少人?
(2)从这6人中随机抽取2人担任本次活动的宣传员,求至少有1人年龄在第3组的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在发生某公共卫生事件期间,有专业机构认为该事件在一段时间没有发生在规模群体感染的标志为“连续10天,每天新增疑似病例不超过7人”。根据过去10天甲、乙、丙、丁四地新增疑似病例数据,一定符合该标志的是 ( )
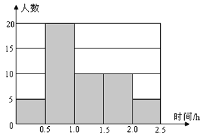
A. 甲地:总体均值为3,中位数为4
B. 乙地:总体均值为1,总体方差大于0
C. 丙地:中位数为2,众数为3
D. 丁地:总体均值为2,总体方差为3
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() 的两个焦点与短轴的一个端点是等边三角形的三个顶点,且长轴长为4.
的两个焦点与短轴的一个端点是等边三角形的三个顶点,且长轴长为4.
(Ⅰ)求椭圆![]() 的方程;
的方程;
(Ⅱ)若![]() 是椭圆
是椭圆![]() 的左顶点,经过左焦点
的左顶点,经过左焦点![]() 的直线
的直线![]() 与椭圆
与椭圆![]() 交于
交于![]() ,
,![]() 两点,求
两点,求![]() 与
与![]() 的面积之差的绝对值的最大值.(
的面积之差的绝对值的最大值.(![]() 为坐标原点)
为坐标原点)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】将函数![]() 的图象向左平移
的图象向左平移![]() 个单位长度,再向上平移1个单位长度,得到函数
个单位长度,再向上平移1个单位长度,得到函数![]() 的图象,则函数
的图象,则函数![]() 具有性质__________.(填入所有正确性质的序号)
具有性质__________.(填入所有正确性质的序号)
①最大值为![]() ,图象关于直线
,图象关于直线![]() 对称;
对称;
②图象关于![]() 轴对称;
轴对称;
③最小正周期为![]() ;
;
④图象关于点![]() 对称;
对称;
⑤在![]() 上单调递减
上单调递减
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com