
【题目】已知函数![]() ,
,
(1)求函数![]() 的单调区间;
的单调区间;
(2)若函数![]() 有两个零点
有两个零点![]() ,(
,(![]() ),求证:
),求证: ![]() .
.
【答案】(1)见解析;(2)见解析.
【解析】试题分析:(1)去绝对值,分为![]() 时,
时, ![]() ,函数单调递增;当
,函数单调递增;当![]() 时,根据导数与0的关系得其单调性;(2)由(1)知,当
时,根据导数与0的关系得其单调性;(2)由(1)知,当![]() 时,函数
时,函数![]() 单调递增,函数至多只有一个零点,不合题意;则必有
单调递增,函数至多只有一个零点,不合题意;则必有![]() ,此时函数
,此时函数![]() 的单调递减区间为
的单调递减区间为![]() ;单调递增区间为
;单调递增区间为![]() ,进一步得出
,进一步得出![]() 和
和![]() ,从而得出答案.
,从而得出答案.
试题解析:(1)依题意有,函数的定义域为![]() ,当
,当![]() 时,
时, ![]() ,
, ![]() ,函数
,函数![]() 的单调增区间为
的单调增区间为![]() , 当
, 当![]() 时,
时, 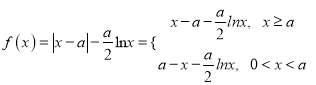 ,若
,若![]() ,
, ![]() ,此时函数单调递增, 若
,此时函数单调递增, 若![]() ,
, ![]() ,此时函数单调递减,综上所述,当
,此时函数单调递减,综上所述,当![]() 时,函数
时,函数![]() 的单调增区间为
的单调增区间为![]() ,当
,当![]() 时,函数
时,函数![]() 的单调减区间为
的单调减区间为![]() ,单调增区间为
,单调增区间为![]()
(2)由(1)知,当![]() 时,函数
时,函数![]() 单调递增,至多只有一个零点,不合题意;则必有
单调递增,至多只有一个零点,不合题意;则必有![]() , 此时函数
, 此时函数![]() 的单调减区间为
的单调减区间为![]() ,单调增区间为
,单调增区间为![]() ,由题意,必须
,由题意,必须![]() ,解得
,解得![]() 由
由![]() ,
, ![]() ,得
,得![]() ,而
,而![]() ,下面证明:
,下面证明: ![]() 时,
时, ![]()
设![]() ,(
,(![]() ),则
),则![]() ,所以
,所以![]() 在
在![]() 时递增,则
时递增,则![]() ,所以
,所以![]() ,又因为
,又因为![]() ,所以
,所以![]() ,综上所述,
,综上所述, ![]() .
.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源: 题型:
【题目】已知函数f(x)=lg(2+x)+lg(2﹣x).
(1)求函数f(x)的定义域并判断函数f(x)的奇偶性;
(2)记函数g(x)=![]() +3x,求函数g(x)的值域;
+3x,求函数g(x)的值域;
(3)若不等式 f(x)>m有解,求实数m的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知数列![]() 的前
的前![]() 项和为
项和为![]() ,
, ![]() ,
, ![]() .等 差数列
.等 差数列![]() 中,
中, ![]() ,且公差
,且公差![]() .
.
(Ⅰ)求数列![]() 的通项公式;
的通项公式;
(Ⅱ)是否存在正整数![]() ,使得
,使得![]() ?.若存在,求出
?.若存在,求出![]() 的最小值;若 不存在,请说明理由.
的最小值;若 不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数y=f(x)是定义在R上的奇函数,当x≥0时,f(x)=2x﹣x2 .
(1)求x<0时f(x)的解析式;
(2)问是否存在正数a,b,当x∈[a,b]时,g(x)=f(x),且g(x)的值域为[ ![]() ,
, ![]() ]?若存在,求出所有的a,b的值,若不存在,请说明理由.
]?若存在,求出所有的a,b的值,若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知中心在原点,焦点在x轴上的椭圆的一个顶点坐标为(0,1),其离心率为 ![]()
(1)求椭圆的标准方程;
(2)椭圆上一点P满足∠F1PF2=60°,其中F1 , F2为椭圆的左右焦点,求△F1PF2的面积.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】2016年3月9日至15日,谷歌人工智能系统“阿尔法”迎战围棋冠军李世石,最终结果“阿尔法”以总比分4比1战胜李世石.许多人认为这场比赛是人类的胜利,也有许多人持反对意见,有网友为此进行了调查,在参加调查的2548名男性中有1560名持反对意见,2452名女性中有1200名持反对意见,在运用这些数据说明“性别”对判断“人机大战是人类的胜利”是否有关系时,应采用的统计方法是( )
A.茎叶图
B.分层抽样
C.独立性检验
D.回归直线方程
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】PM2.5是指悬浮在空气中的空气动力学当量直径小于或等于2.5微米的颗粒物,也称为可入肺颗粒物,根据现行国家标准GB3095﹣2012,PM2.5日均值在35微克/立方米以下空气质量为一级;在35微克/立方米~75毫克/立方米之间空气质量为二级;在75微克/立方米以上空气质量为超标.从某自然保护区2012年全年每天的PM2.5监测值数据中随机地抽取10天的数据作为样本,监测值频数如表所示:
PM2.5日均值 | [25,35] | (35,45] | (45,55] | (55,65] | (65,75] | (75,85] |
频数 | 3 | 1 | 1 | 1 | 1 | 3 |
(1)从这10天的PM2.5日均值监测数据中,随机抽取3天,求恰有1天空气质量达到一级的概率;
(2)从这10天的数据中任取3天数据,记ξ表示抽到PM2.5监测数据超标的天数,求ξ的分布列;
(3)以这10天的PM2.5日均值来估计一年的空气质量状况,则一年(按366天算)中平均有多少天的空气质量达到一级或二级.(精确到整数)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com