
【题目】一半径为4.8米的水轮如图所示,水轮圆心![]() 距离水面2.4米,已知水轮每60秒逆时针转动一圈,如果当水轮上点
距离水面2.4米,已知水轮每60秒逆时针转动一圈,如果当水轮上点![]() 从水中浮现时(图中点
从水中浮现时(图中点![]() )开始计时,则( )
)开始计时,则( )
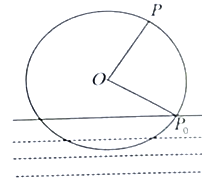
A.点![]() 第一次到达最高点需要10秒
第一次到达最高点需要10秒
B.在水轮转动的一圈内,有20秒的时间,点![]() 距离水面的高度不低于4.8米
距离水面的高度不低于4.8米
C.点![]() 距离水面的高度
距离水面的高度![]() (米)与
(米)与![]() (秒)的函数解析式为
(秒)的函数解析式为![]()
D.当水轮转动50秒时,点![]() 在水面下方,距离水面1.2米
在水面下方,距离水面1.2米
 每日10分钟口算心算速算天天练系列答案
每日10分钟口算心算速算天天练系列答案科目:高中数学 来源: 题型:
【题目】2018年6月14日,国际足联世界杯足球赛在俄罗斯举行了第21届赛事.虽然中国队一如既往地成为了看客,但中国球迷和参赛的32支队伍所在国球迷一样,对本届球赛热情似火,在6月14日开幕式的第二天,我校足球社团从全校学生中随机抽取了120名学生,对是否收看开幕式情况进行了问卷调查,统计数据如下:
收看 | 没收看 | |
男生 | 60 | 20 |
女生 | 20 | 20 |
(1)根据上表说明,能否有99%的把握认为,是否收看开幕式与性别有关?
(2)现从参与问卷调查且收看了开幕式的学生中,采用按性别分层抽样的方法,选取12人参加志愿者宣传活动.
(i)问男、女学生各选取了多少人?
(ⅱ)若从这12人中随机选取3人到校广播站开展足球项目的宣传介绍,设选取的3人中女生人数为X,写出X的分布列,并求![]() .
.
附: ,其中
,其中![]() .
.
| 0.10 | 0.05 | 0.025 | 0.01 | 0.005 |
| 2.706 | 3.841 | 5.024 | 6.635 | 7.879 |
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】以直角坐标系的原点![]() 为极点,
为极点,![]() 轴的正半轴为极轴建立极坐标系,已知点
轴的正半轴为极轴建立极坐标系,已知点![]() 的直角坐标为
的直角坐标为![]() ,若直线
,若直线![]() 的极坐标方程为
的极坐标方程为![]() ,曲线
,曲线![]() 的参数方程是
的参数方程是![]() (
(![]() 为参数).
为参数).
(1)求直线l和曲线![]() 的普通方程;
的普通方程;
(2)设直线l和曲线![]() 交于
交于![]() 两点,求
两点,求![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某城市100户居民的月平均用电量(单位:度),以![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() 分组的频率分布直方图如图所示.
分组的频率分布直方图如图所示.
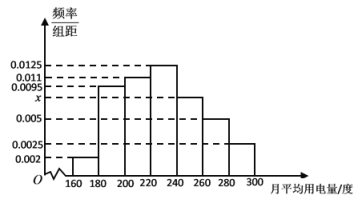
(1)求直方图中![]() 的值;
的值;
(2)求月平均用电量的众数和中位数;
(3)在月平均用电量为![]() ,
,![]() ,
,![]() 的三组用户中,用分层抽样的方法抽取10户居民,则月平均用电量在
的三组用户中,用分层抽样的方法抽取10户居民,则月平均用电量在![]() 的用户中应抽取多少户?
的用户中应抽取多少户?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() ,若存在实数
,若存在实数![]() ,使得等式
,使得等式![]() 对于定义域内的任意实数
对于定义域内的任意实数![]() 均成立,则称函数
均成立,则称函数![]() 为“可平衡”函数,有序数对
为“可平衡”函数,有序数对![]() 称为函数
称为函数![]() 的“平衡”数对.
的“平衡”数对.
(1)若![]() ,判断
,判断![]() 是否为“可平衡”函数,并说明理由;
是否为“可平衡”函数,并说明理由;
(2)若![]() 且
且![]() ,
,![]() 均为
均为![]() 的“可平衡”数对,当
的“可平衡”数对,当![]() 时,方程
时,方程![]() 有两个不相等的实根,求实数
有两个不相等的实根,求实数![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆C:![]() 的焦距为2
的焦距为2![]() ,左顶点与上顶点连线的斜率为
,左顶点与上顶点连线的斜率为![]() .
.
(Ⅰ)求椭圆C的标准方程;
(Ⅱ)过点P(m,0)作圆x2+y2=1的一条切线l交椭圆C于M,N两点,当|MN|的值最大时,求m的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com