
分析 假设存在符合题目要求的实数a.根据x∈A可以求得:C={z|0≤z≤4}、B={y|-2-a≤y≤4-a}.然后由限制性条件“C⊆B”列出关于a的不等式组并解答.
解答 解:假设存在符合题目要求的实数a.
当x∈A时,∵z=x2,
∴0≤z≤4,
∴C={z|0≤z≤4}.
∵y=2x-a,
∴-2-a≤y≤4-a,
∴B={y|-2-a≤y≤4-a}.
欲使C⊆B,则$\left\{\begin{array}{l}{-2-a≤0}\\{4-a≥4}\end{array}\right.$,
∴-2≤a≤0.
故存在实数a,且当-2≤a≤0时,C⊆B.
点评 本题考查了集合的包含关系判断及应用.解答该题需要掌握概念:如果集合A中的任意一个元素都是集合B的元素,那么集合A叫做集合B的子,表示为A⊆B.


科目:高中数学 来源: 题型:选择题
| A. | 充分而不必要条件 | B. | 必要而不充分条件 | ||
| C. | 充分必要条件 | D. | 既不充分也不必要条件 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
| 资金投入x | 2 | 3 | 4 | 5 | 6 |
| 利润y | 2 | 3 | 5 | 6 | 9 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
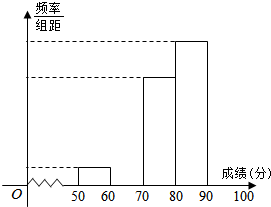 青少年“心理健康”问题越来越引起社会关注,某校对高一600名学生进行了一次“心理健康”知识测试,并从中抽取了部分学生的成绩(得分取正整数,满分100分)作为样本,绘制了下面尚未完成的频率分布表和频率分布直方图.
青少年“心理健康”问题越来越引起社会关注,某校对高一600名学生进行了一次“心理健康”知识测试,并从中抽取了部分学生的成绩(得分取正整数,满分100分)作为样本,绘制了下面尚未完成的频率分布表和频率分布直方图.| 分组 | 频数 | 频率 |
| [50,60) | 2 | 0.04 |
| [60,70) | 8 | 0.16 |
| [70,80) | 10 | |
| [80,90) | ||
| [90,100] | 14 | 0.28 |
| 合计 | 1.00 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
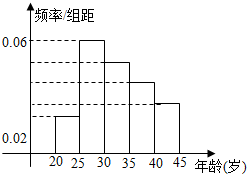 某居民小区年龄在20岁到45岁的居民共有150人,如图是他们上网情况的频率分布直方图,现已知年龄在[30,35),[40,45]的人数分别是39、21人,则年龄在[35,40)的频数( )
某居民小区年龄在20岁到45岁的居民共有150人,如图是他们上网情况的频率分布直方图,现已知年龄在[30,35),[40,45]的人数分别是39、21人,则年龄在[35,40)的频数( )| A. | 6 | B. | 9 | C. | 30 | D. | 45 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
| 等级 | 优秀 | 合格 | 尚待改进 |
| 频数 | 15 | x | 5 |
| 等级 | 优秀 | 合格 | 尚待改进 |
| 频数 | 15 | 3 | y |
| 男生 | 女生 | 总计 | |
| 优秀 | |||
| 非优秀 | |||
| 总计 |
| P(K2≥k0) | 0.10 | 0.05 | 0.010 | 0.005 |
| k0 | 2.706 | 3.841 | 6.635 | 7.879 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com