
【题目】在平面直角坐标系![]() 中,已知
中,已知![]() 为三个不同的定点.以原点
为三个不同的定点.以原点![]() 为圆心的圆与线段
为圆心的圆与线段![]() 都相切.
都相切.
(Ⅰ)求圆![]() 的方程及
的方程及![]() 的值;
的值;
(Ⅱ)若直线![]() 与圆
与圆![]() 相交于
相交于![]() 两点,且
两点,且![]() ,求
,求![]() 的值;
的值;
(Ⅲ)在直线![]() 上是否存在异于
上是否存在异于![]() 的定点
的定点![]() ,使得对圆
,使得对圆![]() 上任意一点
上任意一点![]() ,都有
,都有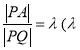 为常数
为常数![]() ?若存在,求出点
?若存在,求出点![]() 的坐标及
的坐标及![]() 的值;若不存在,请说明理由.
的值;若不存在,请说明理由.
【答案】(Ⅰ)![]() ,
,![]()
![]() ;(Ⅱ)
;(Ⅱ)![]() ;(Ⅲ)见解析
;(Ⅲ)见解析
【解析】
(Ⅰ)根据直线与圆相切,圆心到直线的距离等于半径求解;(Ⅱ)用坐标表示向量积,再联立直线与圆方程,消元代入向量积求解;(Ⅲ)假设A、P的坐标,根据两点距离公式与![]() 建立等式,再根据A、P分别满足直线和圆的方程化简等式,最后根据等式恒成立的条件求解.
建立等式,再根据A、P分别满足直线和圆的方程化简等式,最后根据等式恒成立的条件求解.
(Ⅰ)由于圆![]() 与线段
与线段![]() 相切,所以半径
相切,所以半径![]() .
.
即圆![]() 的方程为
的方程为![]() .
.
又由题![]() 与线段
与线段![]() 相切,
相切,
所以线段![]() 方程为
方程为![]() .即
.即![]() .
.
故直线![]() 的方程为
的方程为![]() .
.
由直线![]() 和圆
和圆![]() 相切可得:
相切可得: ,
,
解得![]() 或
或![]() .由于
.由于![]() 为不同的点,所以
为不同的点,所以![]() .
.
(Ⅱ)设![]() ,
,![]() ,则
,则![]() .
.
由![]() 可得
可得![]() ,
,
![]() ,解得
,解得![]() .所以
.所以![]() .
.
故![]() .
.
所以![]() .所以
.所以![]() .
.
故![]() .
.
(Ⅲ)设![]() .
.
则![]() ,
,![]() .
.
若在直线![]() 上存在异于
上存在异于![]() 的定点
的定点![]() ,使得对圆
,使得对圆![]() 上任意一点
上任意一点![]() ,
,
都有 为常数
为常数![]() ,
,
等价于 对圆
对圆![]() 上任意点
上任意点![]() 恒成立.
恒成立.
即![]() .
.
整理得![]() .
.
因为点![]() 在直线
在直线![]() 上,所以
上,所以![]() .
.
由于![]() 在圆
在圆![]() 上,所以
上,所以![]() .
.
故![]() 对任意
对任意![]() 恒成立.
恒成立.
所以 显然
显然![]() ,所以
,所以![]() .
.
故![]() ,
,
因为![]() ,解得
,解得![]() 或
或![]() .
.
当![]() 时,
时,![]() ,此时
,此时![]() 重合,舍去.
重合,舍去.
当![]() 时,
时,![]() ,
,
综上,存在满足条件的定点![]() ,此时
,此时![]() .
.


科目:高中数学 来源: 题型:
【题目】在正整数数列中,由1开始按如下规则依次取它的项:第一次取1;第二次取2个连续偶数![]() ;第三次取3个连续奇数
;第三次取3个连续奇数![]() ;第四次取4个连续偶数
;第四次取4个连续偶数![]() ;第五次取5个连续奇数
;第五次取5个连续奇数![]() ;……按此规律取下去,得到一个子数列
;……按此规律取下去,得到一个子数列![]() ,
,![]() ,……则在这个子数列中,第
,……则在这个子数列中,第![]() 个数是( )
个数是( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,已知正四面体D﹣ABC(所有棱长均相等的三棱锥),P、Q、R分别为AB、BC、CA上的点,AP=PB, ![]() =
= ![]() =2,分别记二面角D﹣PR﹣Q,D﹣PQ﹣R,D﹣QR﹣P的平面角为α、β、γ,则( )
=2,分别记二面角D﹣PR﹣Q,D﹣PQ﹣R,D﹣QR﹣P的平面角为α、β、γ,则( )
A.γ<α<β
B.α<γ<β
C.α<β<γ
D.β<γ<α
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在三棱柱ABC–A1B1C1中,AB=BC,D为AC的中点,O为四边形B1C1CB的对角线的交点,AC⊥BC1.求证:
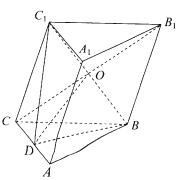
(1)OD∥平面A1ABB1;
(2)平面A1C1CA⊥平面BC1D.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】共享单车已成为一种时髦的新型环保交通工具,某共享单车公司为了拓展市场,对![]() ,
,![]() 两个品牌的共享单车在编号分别为1,2,3,4,5的五个城市的用户人数(单位:十万)进行统计,得到数据如下:
两个品牌的共享单车在编号分别为1,2,3,4,5的五个城市的用户人数(单位:十万)进行统计,得到数据如下:
城市品牌 | 1 | 2 | 3 | 4 | 5 |
| 3 | 4 | 12 | 6 | 8 |
| 4 | 3 | 7 | 9 | 5 |
(Ⅰ)若共享单车用户人数超过50万的城市称为“优城”,否则称为“非优城”,据此判断能否有![]() 的把握认为“优城”和共享单车品牌有关?
的把握认为“优城”和共享单车品牌有关?
(Ⅱ)若不考虑其它因素,为了拓展市场,对![]() 品牌要从这五个城市选择三个城市进行宣传.
品牌要从这五个城市选择三个城市进行宣传.
(i)求城市2被选中的概率;
(ii)求在城市2被选中的条件下城市3也被选中的概率.
附:参考公式及数据
| 0.15 | 0.10 | 0.05 | 0.025 | 0.005 | 0.001 | |
| 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】“![]() 三个内角的度数可以构成等差数列”是“
三个内角的度数可以构成等差数列”是“![]() 中有一个内角为
中有一个内角为![]() ”的( )
”的( )
A. 充分不必要条件B. 必要不充分条件
C. 充要条件D. 既不充分也不必要条件
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】(本题满分14分)本题共有2个小题,第1小题满分6分,第2小题满分8分
沙漏是古代的一种计时装置,它由两个形状完全相同的容器和一个狭窄的连接管道组成,开始时细沙全部在上部容器中,细沙通过连接管道全部流到下部容器所需要的时间称为该沙漏的一个沙时。如图,某沙漏由上下两个圆锥组成,圆锥的底面直径和高均为8cm,细沙全部在上部时,其高度为圆锥高度的![]() (细管长度忽略不计).
(细管长度忽略不计).
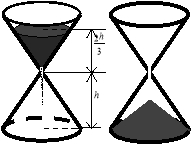
(1)如果该沙漏每秒钟漏下0.02cm3的沙,则该沙漏的一个沙时为多少秒(精确到1秒)?
(2)细沙全部漏入下部后,恰好堆成个一盖住沙漏底部的圆锥形沙堆,求此锥形沙堆的高度(精确到0.1cm).
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】为缓解交通运行压力,某市公交系统实施疏堵工程.现调取某路公交车早高峰时段全程运输时间(单位:分钟)的数据,从疏堵工程完成前的数据中随机抽取5个数据,记为![]() 组;从疏堵工程完成后的数据中随机抽取5个数据,记为
组;从疏堵工程完成后的数据中随机抽取5个数据,记为![]() 组.
组.
![]() 组:
组:![]()
![]()
![]()
![]()
![]()
![]() 组:
组:![]()
![]()
![]()
![]()
![]()
(Ⅰ)该路公交车全程运输时间不超过![]() 分钟,称为“正点运行”.从
分钟,称为“正点运行”.从![]() ,
,![]() 两组数据中各随机抽取一个数据,求这两个数据对应的两次运行中至少有一次“正点运行”的概率;
两组数据中各随机抽取一个数据,求这两个数据对应的两次运行中至少有一次“正点运行”的概率;
(Ⅱ)试比较![]() ,
,![]() 两组数据方差的大小(不要求计算),并说明其实际意义.
两组数据方差的大小(不要求计算),并说明其实际意义.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com