
【题目】已知函数![]() .
.
(1)求函数![]() 在点
在点![]() 处的切线方程;
处的切线方程;
(2)求函数![]() 在
在![]() 上的值域;
上的值域;
(3)若存在![]() ,使得
,使得![]() 成立,求
成立,求![]() 的最大值.(其中自然常数
的最大值.(其中自然常数![]() )
)
【答案】(1)![]() (2)
(2)![]() (3)
(3)![]() 的最大值为6.
的最大值为6.
【解析】
)(1)对![]() 求导得到
求导得到![]() ,然后代入切点横坐标,得到斜率,点斜式写出切线方程,整理得答案;(2)利用导数判断出
,然后代入切点横坐标,得到斜率,点斜式写出切线方程,整理得答案;(2)利用导数判断出![]() 的单调性,根据单调性求出其最小值,并比较在两个端点时的函数值,得到最大值,从而得到答案;(3)由(2)可得
的单调性,根据单调性求出其最小值,并比较在两个端点时的函数值,得到最大值,从而得到答案;(3)由(2)可得![]() ,要使
,要使![]() 成立,且
成立,且![]() 的值最大,则
的值最大,则![]() ,
,![]() …
…![]() 的值应最小,即
的值应最小,即![]() ,
,![]() ,从而得到
,从而得到![]() ,从而得到
,从而得到![]() 的最大值为
的最大值为![]() .
.
解:(1)![]() ,
,
∴![]() ,又
,又![]() ,
,
∴![]() ,即
,即![]() 为所求切线的方程.
为所求切线的方程.
(2)![]()
令![]() ,得
,得![]() (舍去负根)
(舍去负根)
所以![]() 时,
时,![]() ,
,![]() 单调递减,
单调递减,
![]() 时,
时,![]() ,
,![]() 单调递增.
单调递增.
故![]() ,
,
又因为![]() ,
,
![]() ,
,
故![]() ,
,
故![]() 时,
时,![]() .
.
(3)由(2)知,![]() 时,
时,![]() .
.
所以有![]()
而要使![]() 成立,且
成立,且![]() 的值最大,
的值最大,
则![]() ,
,![]() …
…![]() 每个的函数值应最小,
每个的函数值应最小,
即,即![]() ,
,![]() ,
,
从而得到![]() ,
,
所以![]() ,
,
所以![]() 的最大值为
的最大值为![]() .
.


科目:高中数学 来源: 题型:
【题目】在平面直角坐标系![]() 中,已知曲线
中,已知曲线![]() 的参数方程为
的参数方程为![]() (
(![]() 为参数),以坐标原点
为参数),以坐标原点![]() 为极点,以
为极点,以![]() 轴的正半轴为极轴,建立极坐标系,曲线
轴的正半轴为极轴,建立极坐标系,曲线![]() 的极坐标方程为
的极坐标方程为![]() .
.
(1)设点![]() 分别为曲线
分别为曲线![]() 与曲线
与曲线![]() 上的任意一点,求
上的任意一点,求![]() 的最大值;
的最大值;
(2)设直线![]() (
(![]() 为参数)与曲线
为参数)与曲线![]() 交于
交于![]() 两点,且
两点,且![]() ,求直线
,求直线![]() 的普通方程.
的普通方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某同学研究曲线![]() 的性质,得到如下结论:①
的性质,得到如下结论:①![]() 的取值范围是
的取值范围是![]() ;②曲线
;②曲线![]() 是轴对称图形;③曲线
是轴对称图形;③曲线![]() 上的点到坐标原点的距离的最小值为
上的点到坐标原点的距离的最小值为![]() . 其中正确的结论序号为( )
. 其中正确的结论序号为( )
A.①②B.①③C.②③D.①②③
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】尽管目前人类还无法准确预报地震,但科学家通过研究,已经对地震有所了解,例如,地震释放出的能量![]() (单位:焦耳)与地震里氏震级
(单位:焦耳)与地震里氏震级![]() 之间的关系为
之间的关系为![]() .
.
(1)已知地震等级划分为里氏![]() 级,根据等级范围又分为三种类型,其中小于
级,根据等级范围又分为三种类型,其中小于![]() 级的为“小地震”,介于
级的为“小地震”,介于![]() 级到
级到![]() 级之间的为“有感地震”,大于
级之间的为“有感地震”,大于![]() 级的为“破坏性地震”若某次地震释放能量约
级的为“破坏性地震”若某次地震释放能量约![]() 焦耳,试确定该次地震的类型;
焦耳,试确定该次地震的类型;
(2)2008年汶川地震为里氏![]() 级,2011年日本地震为里氏
级,2011年日本地震为里氏![]() 级,问:2011年日本地震所释放的能量是2008年汶川地震所释放的能量的多少倍? (取
级,问:2011年日本地震所释放的能量是2008年汶川地震所释放的能量的多少倍? (取![]() )
)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() :
:![]() 的焦点分别为
的焦点分别为![]() ,
,![]() ,椭圆
,椭圆![]() 的离心率为
的离心率为![]() ,且经过点
,且经过点![]() ,经过
,经过![]() ,
,![]() 作平行直线
作平行直线![]() ,
,![]() ,交椭圆
,交椭圆![]() 于两点
于两点![]() ,
,![]() 和两点
和两点![]() ,
,![]() .
.
(1)求![]() 的方程;
的方程;
(2)求四边形![]() 面积的最大值.
面积的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系![]() 中,以
中,以![]() 为极点,
为极点,![]() 轴的非负半轴为极轴,建立极坐标系,曲线
轴的非负半轴为极轴,建立极坐标系,曲线![]() 的极坐标方程为
的极坐标方程为![]() ,直线
,直线![]() 的参数方程为
的参数方程为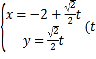 为参数
为参数![]() ,直线
,直线![]() 与曲线
与曲线![]() 分别交于
分别交于![]() 两点.
两点.
(1)若点![]() 的极坐标为
的极坐标为![]() ,求
,求![]() 的值;
的值;
(2)求曲线![]() 的内接矩形周长的最大值.
的内接矩形周长的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】(2017高考新课标Ⅲ,理19)如图,四面体ABCD中,△ABC是正三角形,△ACD是直角三角形,∠ABD=∠CBD,AB=BD.

(1)证明:平面ACD⊥平面ABC;
(2)过AC的平面交BD于点E,若平面AEC把四面体ABCD分成体积相等的两部分,求二面角D–AE–C的余弦值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com