
【题目】如图,在直三棱柱![]() 中,
中,![]() ,
,![]() 是
是![]() 的中点,
的中点,![]() .
.
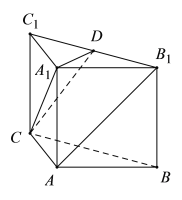
(1)求证:![]() 平面
平面![]() ;
;
(2)若异面直线![]() 和
和![]() 所成角为
所成角为![]() ,求四棱锥
,求四棱锥![]() 的体积.
的体积.
 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:
【题目】已知![]() 是给定的平面,设不在
是给定的平面,设不在![]() 内的任意两点M,N所在的直线为l,则下列命题正确的是( )
内的任意两点M,N所在的直线为l,则下列命题正确的是( )
A.在![]() 内存在直线与直线l异面
内存在直线与直线l异面
B.在![]() 内存在直线与直线l相交
内存在直线与直线l相交
C.在![]() 内存在直线与直线l平行
内存在直线与直线l平行
D.存在过直线l的平面与![]() 平行
平行
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】![]() 时代悄然来临,为了研究中国手机市场现状,中国信通院统计了2019年手机市场每月出货量以及与2018年当月同比增长的情况,得到如下统计图,根据该统计图,下列说法错误的是( )
时代悄然来临,为了研究中国手机市场现状,中国信通院统计了2019年手机市场每月出货量以及与2018年当月同比增长的情况,得到如下统计图,根据该统计图,下列说法错误的是( )
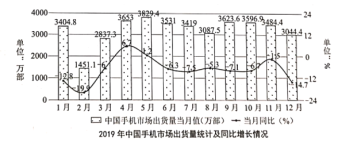
A.2019年全年手机市场出货量中,5月份出货量最多
B.2019年下半年手机市场各月份出货量相对于上半年各月份波动小
C.2019年全年手机市场总出货量低于2018年全年总出货量
D.2018年12月的手机出货量低于当年8月手机出货量
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】动点![]() 与定点
与定点![]() 的距离和该动点到直线
的距离和该动点到直线![]() 的距离的比是常数
的距离的比是常数![]() .
.
(1)求动点![]() 轨迹方程
轨迹方程![]() ;
;
(2)已知点![]() ,问在
,问在![]() 轴上是否存在一点
轴上是否存在一点![]() ,使得过
,使得过![]() 点的任一条斜率不为0的弦交曲线
点的任一条斜率不为0的弦交曲线![]() 于
于![]() 两点,都有
两点,都有![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】甲、乙两位同学参加某个知识答题游戏节目,答题分两轮,第一轮为“选题答题环节”第二轮为“轮流坐庄答题环节”.首先进行第一轮“选题答题环节”,答题规则是:每位同学各自从备选的5道不同题中随机抽出3道题进行答题,答对一题加10分,答错一题(不答视为答错)减5分,已知甲能答对备选5道题中的每道题的概率都是![]() ,乙恰能答对备选5道题中的其中3道题;第一轮答题完毕后进行第二轮“轮流坐庄答题环节”,答题规则是:先确定一人坐庄答题,若答对,继续答下一题…,直到答错,则换人(换庄)答下一题…以此类推.例如若甲首先坐庄,则他答第1题,若答对继续答第2题,如果第2题也答对,继续答第3题,直到他答错则换成乙坐庄开始答下一题,…直到乙答错再换成甲坐庄答题,依次类推两人共计答完20道题游戏结束,假设由第一轮答题得分期望高的同学在第二轮环节中最先开始作答,且记第
,乙恰能答对备选5道题中的其中3道题;第一轮答题完毕后进行第二轮“轮流坐庄答题环节”,答题规则是:先确定一人坐庄答题,若答对,继续答下一题…,直到答错,则换人(换庄)答下一题…以此类推.例如若甲首先坐庄,则他答第1题,若答对继续答第2题,如果第2题也答对,继续答第3题,直到他答错则换成乙坐庄开始答下一题,…直到乙答错再换成甲坐庄答题,依次类推两人共计答完20道题游戏结束,假设由第一轮答题得分期望高的同学在第二轮环节中最先开始作答,且记第![]() 道题也由该同学(最先答题的同学)作答的概率为
道题也由该同学(最先答题的同学)作答的概率为![]() (
(![]() ),其中
),其中![]() ,已知供甲乙回答的20道题中,甲,乙两人答对其中每道题的概率都是
,已知供甲乙回答的20道题中,甲,乙两人答对其中每道题的概率都是![]() ,如果某位同学有机会答第
,如果某位同学有机会答第![]() 道题且回答正确则该同学加10分,答错(不答视为答错)则减5分,甲乙答题相互独立;两轮答题完毕总得分高者胜出.回答下列问题
道题且回答正确则该同学加10分,答错(不答视为答错)则减5分,甲乙答题相互独立;两轮答题完毕总得分高者胜出.回答下列问题
(1)请预测第二轮最先开始作答的是谁?并说明理由
(2)①求第二轮答题中![]() ,
,![]() ;
;
②求证![]() 为等比数列,并求
为等比数列,并求![]() (
(![]() )的表达式.
)的表达式.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() 的左、右焦点为
的左、右焦点为![]() 的坐标满足圆
的坐标满足圆![]() 方程
方程![]() ,且圆心
,且圆心![]() 满足
满足![]() .
.
(1)求椭圆![]() 的方程;
的方程;
(2)过点![]() 的直线
的直线![]() 交椭圆
交椭圆![]() 于
于![]() 、
、![]() 两点,过
两点,过![]() 与
与![]() 垂直的直线
垂直的直线![]() 交圆
交圆![]() 于
于![]() 、
、![]() 两点,
两点,![]() 为线段
为线段![]() 中点,若
中点,若![]() 的面积
的面积 ![]() ,求
,求![]() 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() 的左右焦点为
的左右焦点为![]() ,
,![]() ,离心率为
,离心率为![]() ,过点
,过点![]() 且垂直于
且垂直于![]() 轴的直线被椭圆
轴的直线被椭圆![]() 截得的弦长为1.
截得的弦长为1.
(1)求椭圆![]() 的方程;
的方程;
(2)若直线![]() 交椭圆
交椭圆![]() 于点
于点![]() ,
,![]() 两点,与线段
两点,与线段![]() 和椭圆短轴分别交于两个不同点
和椭圆短轴分别交于两个不同点![]() ,
,![]() ,且
,且![]() ,求
,求![]() 的最小值.
的最小值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com