
判断下列命题的真假:
(1)两个平面垂直,过其中一个平面内一点作与它们交线垂直的直线,必垂直于另一个平面;
(2)两个平面垂直,分别在这两个平面内且互相垂直的两直线,一定分别与另一平面垂直;
(3)两平面垂直,分别在这两个平面内的两直线互相垂直.
|
若该点在两个平面的交线上,则命题是错误的,如图 (1),正方体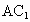 中,平面AC上平面 中,平面AC上平面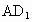 ,平面AC∩平面 ,平面AC∩平面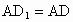 ,在AD上取点A,连结 ,在AD上取点A,连结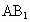 ,则 ,则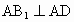 ,即过棱上一点A的直线与棱垂直,但 ,即过棱上一点A的直线与棱垂直,但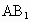 与平面ABCD不垂直,其错误的原因是 与平面ABCD不垂直,其错误的原因是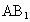 没有保证在平面 没有保证在平面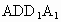 内.可以看出线在面内这一条件的重要性. 内.可以看出线在面内这一条件的重要性.
(2) 该命题注意了直线在平面内,但不能保证这两条直线都与棱垂直,如图,在正方体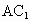 中,平面 中,平面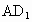 ⊥平面AC,ADl ⊥平面AC,ADl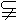 平面 平面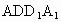 ,AB ,AB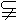 平面ABCD,且 平面ABCD,且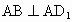 ,即AB与 ,即AB与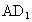 相互垂直,但 相互垂直,但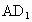 与平面ABCD不垂直. 与平面ABCD不垂直.
(3) 如图(2),正方体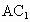 中,平面 中,平面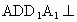 平面ABCD, 平面ABCD,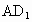 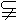 平面 平面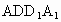 ,AC ,AC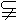 平面ABCD, 平面ABCD,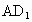 与AC所成的角为60°,即 与AC所成的角为60°,即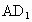 与AC不垂直.各种定理成立的条件是很严格的,只有同时具备才能保证成立. 与AC不垂直.各种定理成立的条件是很严格的,只有同时具备才能保证成立.
点拨:必须注意两个平面垂直的性质定理成立的条件:①线的面内,②线垂直于交线,从而可得出线面垂直. |


科目:高中数学 来源: 题型:
查看答案和解析>>
科目:高中数学 来源: 题型:
查看答案和解析>>
科目:高中数学 来源: 题型:
查看答案和解析>>
科目:高中数学 来源: 题型:
|
|
| b |
| a |
| b+x |
| a+x |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com