
某公司计划2011年在甲、乙两个电视台做总时间不超过300分钟的广告,广告费用不超过9万元.甲、乙电视台的广告收费标准分别为500元/分钟和200元/分钟.假定甲、乙两个电视台为该公司每分钟所做的广告,能给公司带来的收益分别为0.3 万元和0.2万元.问:该公司如何分配在甲、乙两个电视台的广告时间,才能使公司收益最大,最大收益是多少万元?
该公司在甲电视台做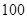 分钟广告,在乙电视台做
分钟广告,在乙电视台做 分钟广告,公司的收益最大,最大收益是
分钟广告,公司的收益最大,最大收益是 万元.
万元.
解析试题分析:由题意可知,若设公司在甲电视台和乙电视台做广告的时间分别为 分钟和
分钟和 分钟,总收益为
分钟,总收益为 元,则可得
元,则可得 ,
, ,从而问题就等价于在线性约束条件
,从而问题就等价于在线性约束条件 下,求线性目标函数
下,求线性目标函数 ,作出不等式组所表示的可行域,在作出直线
,作出不等式组所表示的可行域,在作出直线 ,通过平移直线,即可知,使目标函数取得最大值的点为直线
,通过平移直线,即可知,使目标函数取得最大值的点为直线 与直线
与直线 的交点
的交点 ,从而得到该公司在甲电视台做
,从而得到该公司在甲电视台做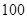 分钟广告,在乙电视台做
分钟广告,在乙电视台做 分钟广告,公司的收益最大,最大收益是
分钟广告,公司的收益最大,最大收益是 万元.
万元.
试题解析:设公司在甲电视台和乙电视台做广告的时间分别为 分钟和
分钟和 分钟,总收益为
分钟,总收益为 元,由题意得:
元,由题意得: ,
, , 6分
, 6分
不等式组等价于 ,作出二元一次不等式组所表示的平面区域,即可行域,如图:
,作出二元一次不等式组所表示的平面区域,即可行域,如图:
作直线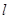 :
: ,即
,即 , 8分
, 8分
平移直线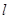 ,从图中可知,当直线过点
,从图中可知,当直线过点 时,目标函数取得最大值,
时,目标函数取得最大值,
联立 , 8分
, 8分
∴点 的坐标为
的坐标为 ,∴
,∴ (元), 11分
(元), 11分
∴该公司在甲电视台做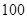 分钟广告,在乙电视台做
分钟广告,在乙电视台做 分钟广告,公司的收益最大,最大收益是
分钟广告,公司的收益最大,最大收益是 万元.
万元.
考点:线性规划的运用.


 新思维假期作业暑假吉林大学出版社系列答案
新思维假期作业暑假吉林大学出版社系列答案 蓝天教育暑假优化学习系列答案
蓝天教育暑假优化学习系列答案科目:高中数学 来源: 题型:解答题
(2013·黄山模拟)若x,y满足约束条件
(1)求目标函数z= x-y+
x-y+ 的最值.
的最值.
(2)若目标函数z=ax+2y仅在点(1,0)处取得最小值,求a的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
某营养师要为某个儿童预订午餐和晚餐,已知一个单位的午餐含 个单位的碳水化合物,
个单位的碳水化合物, 个单位的蛋白质和
个单位的蛋白质和 个单位的维生素
个单位的维生素 ;一个单位的晚餐含
;一个单位的晚餐含 个单位的碳水化合物,
个单位的碳水化合物, 个单位的蛋白质和
个单位的蛋白质和 个单位的维生素
个单位的维生素 .另外,该儿童这两餐需要的营养中至少含
.另外,该儿童这两餐需要的营养中至少含 个单位的碳水化合物,
个单位的碳水化合物, 个单位的蛋白质和
个单位的蛋白质和 个单位的维生素
个单位的维生素 .如果一个单位的午餐、晚餐的费用分别是
.如果一个单位的午餐、晚餐的费用分别是 元和
元和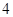 元,那么要满足上述的营养要求,并且花费最少,应当为该儿童分别预订多少个单位的午餐和晚餐?
元,那么要满足上述的营养要求,并且花费最少,应当为该儿童分别预订多少个单位的午餐和晚餐?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com