
【题目】已知函数![]()
(1)若![]() ,求
,求![]() 的极值;
的极值;
(2)若![]() ,都有
,都有![]() 成立,求k的取值范围.
成立,求k的取值范围.
科目:高中数学 来源: 题型:
【题目】如图为某市国庆节7天假期的商品房日认购量(单位:套)与日成交量(单位:套)的折线图,则下面结论中正确的是( )
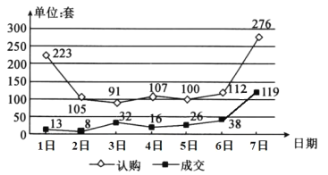
A.日成交量的中位数是16
B.日成交量超过日平均成交量的有1天
C.日认购量与日期是正相关关系
D.日认购量的方差大于日成交量的方差
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】追求人类与生存环境的和谐发展是中国特色社会主义生态文明的价值取向.为了改善空气质量,某城市环保局随机抽取了一年内100天的空气质量指数(![]() )的检测数据,结果统计如下:
)的检测数据,结果统计如下:
|
|
|
|
|
|
|
空气质量 | 优 | 良 | 轻度污染 | 中度污染 | 重度污染 | 严重污染 |
天数 | 6 | 14 | 18 | 27 | 25 | 10 |
(1)从空气质量指数属于![]() ,
,![]() 的天数中任取3天,求这3天中空气质量至少有2天为优的概率;
的天数中任取3天,求这3天中空气质量至少有2天为优的概率;
(2)已知某企业每天的经济损失![]() (单位:元)与空气质量指数
(单位:元)与空气质量指数![]() 的关系式为
的关系式为 ,试估计该企业一个月(按30天计算)的经济损失的数学期望.
,试估计该企业一个月(按30天计算)的经济损失的数学期望.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() 的焦距为2,过点
的焦距为2,过点![]() .
.
(1)求椭圆![]() 的标准方程;
的标准方程;
(2)设椭圆的右焦点为F,定点![]() ,过点F且斜率不为零的直线l与椭圆交于A,B两点,以线段AP为直径的圆与直线
,过点F且斜率不为零的直线l与椭圆交于A,B两点,以线段AP为直径的圆与直线![]() 的另一个交点为Q,证明:直线BQ恒过一定点,并求出该定点的坐标.
的另一个交点为Q,证明:直线BQ恒过一定点,并求出该定点的坐标.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知![]() 为常数,
为常数, ![]() ,函数
,函数![]() ,
, ![]() (其中
(其中![]() 是自然对数的底数).
是自然对数的底数).
(1)过坐标原点![]() 作曲线
作曲线![]() 的切线,设切点为
的切线,设切点为![]() ,求证:
,求证: ![]() ;
;
(2)令![]() ,若函数
,若函数![]() 在区间
在区间![]() 上是单调函数,求
上是单调函数,求![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知抛物线![]() 焦点为
焦点为![]() ,直线
,直线![]() 过
过![]() 与抛物线交于
与抛物线交于![]() 两点.
两点.![]() 到准线的距离之和最小为8.
到准线的距离之和最小为8.
(1)求抛物线方程;
(2)若抛物线上一点![]() 纵坐标为
纵坐标为![]() ,直线
,直线![]() 分别交准线于
分别交准线于![]() .求证:以
.求证:以![]() 为直径的圆过焦点
为直径的圆过焦点![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】选修4-4:坐标系与参数方程
在直角坐标系![]() 中,曲线
中,曲线![]() 的参数方程为
的参数方程为![]() (
(![]() 为参数),以坐标原点
为参数),以坐标原点![]() 为极点,
为极点,![]() 轴正半轴为极轴建立极坐标系,曲线
轴正半轴为极轴建立极坐标系,曲线![]() 的极坐标方程为
的极坐标方程为![]() ,且曲线
,且曲线![]() 与
与![]() 恰有一个公共点.
恰有一个公共点.
(Ⅰ)求曲线![]() 的极坐标方程;
的极坐标方程;
(Ⅱ)已知曲线![]() 上两点
上两点![]() ,
,![]() 满足
满足![]() ,求
,求![]() 面积的最大值.
面积的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=(k+![]() )lnx+
)lnx+![]() ,k∈[4,+∞),曲线y=f(x)上总存在两点M(x1,y1),N(x2,y2),使曲线y=f(x)在M,N两点处的切线互相平行,则x1+x2的取值范围为
,k∈[4,+∞),曲线y=f(x)上总存在两点M(x1,y1),N(x2,y2),使曲线y=f(x)在M,N两点处的切线互相平行,则x1+x2的取值范围为
A. (![]() ,+∞) B. (
,+∞) B. (![]() ,+∞) C. [
,+∞) C. [![]() ,+∞) D. [
,+∞) D. [![]() ,+∞)
,+∞)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com