
【题目】已知函数![]()
(Ⅰ)若![]() ,求
,求![]() 在
在![]() 处的切线方程;
处的切线方程;
(Ⅱ)证明:对任意正数![]() ,函数
,函数![]() 和
和![]() 的图像总有两个公共点.
的图像总有两个公共点.
【答案】(Ⅰ) ![]() ;(Ⅱ)证明见解析.
;(Ⅱ)证明见解析.
【解析】试题分析:(I)先根据导数几何意义得切线的斜率![]() ,再根据点斜式得切线方程;(Ⅱ)函数
,再根据点斜式得切线方程;(Ⅱ)函数![]() 和
和![]() 的图像总有两个公共点,等价于
的图像总有两个公共点,等价于![]()
![]() 总有两个实数根.变量分离得
总有两个实数根.变量分离得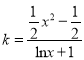 ,再根据导数研究函数
,再根据导数研究函数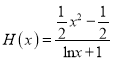 单调性,结合图像确定有两个交点的条件,即得证.
单调性,结合图像确定有两个交点的条件,即得证.
试题解析:(I)![]() 时,则
时,则![]()
![]() 在
在![]() 处的切线的斜率
处的切线的斜率![]()
又![]() 时,
时, ![]() 即切点
即切点![]() ,
,
所以![]() 在
在![]() 处的切线方程为:
处的切线方程为:
![]() ,即
,即![]()
(Ⅱ)法一:
记![]()
则![]() (已知
(已知![]() ).
).
因为![]() 有意义,
有意义, ![]()
所以![]()
所以![]() 在
在![]() 单调递减,在
单调递减,在![]() 单调递增,
单调递增,
故![]()
记![]()
![]()
因为![]()
所以![]() 在
在![]() 单调递增,在
单调递增,在![]() 单调递减,
单调递减,
故![]()
故![]() 恒成立,即
恒成立,即![]()
又![]() 时,
时, ![]() 时,
时, ![]() ,
,
故![]() 在
在![]() 和
和![]() 各有一个零点,
各有一个零点,
即![]() 和
和![]() 的图像在
的图像在![]() 和
和![]() 各有且只有一个公共点.
各有且只有一个公共点.
法二:函数![]() 和
和![]() 的图像总有两个公共点,等价于
的图像总有两个公共点,等价于![]()
![]() 总有两个实数根.
总有两个实数根.
![]()
![]() 显示
显示![]() 不是该方程的根.
不是该方程的根.
当![]() 时,
时, 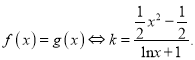
记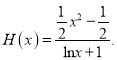
则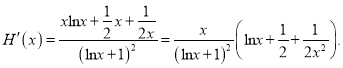
再记![]()
因为![]()
所以![]() 在
在![]() 单调递增,在
单调递增,在![]() 单调递减
单调递减
所以![]()
即![]()
从而![]() 在
在![]() 和
和![]() 均单调递增,
均单调递增,
又![]() 时,
时, ![]() 时,
时, ![]() 时,
时, ![]() ,
,
又![]() 时,
时, ![]() 时,
时, ![]() 时,
时, ![]() ,
,
![]() 的草图如图:
的草图如图:
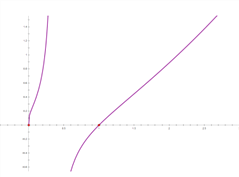
故对任意的正数![]() ,直线
,直线![]() 与
与![]() 的图像总有两个公共点,
的图像总有两个公共点,
即方程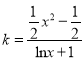 总有两个根,
总有两个根,
即函数![]() 和
和![]() 的图像总有两个公共点,命题得证.
的图像总有两个公共点,命题得证.


 名校课堂系列答案
名校课堂系列答案科目:高中数学 来源: 题型:
【题目】如图,四边形ABCD内接于⊙O,过点A作⊙O的切线EP交CB的延长线于P,∠PAB=35°. 
(1)若BC是⊙O的直径,求∠D的大小;
(2)若∠PAB=35°,求证: ![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在四棱锥P-ABCD中,底面ABCD为菱形,∠BAD=60°,Q为AD的中点.
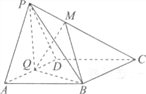
(Ⅰ)若PA=PD,求证:平面PQB⊥平面PAD;
(Ⅱ)点M在线段PC上,PM=tPC,试确定实数t的值,使PA∥平面MQB;
(Ⅲ)在(Ⅱ)的条件下,若平面PAD⊥平面ABCD,且PA=PD=AD=2,求二面角M-BQ-C的大小.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某运输公司有7辆可载![]() 的
的![]() 型卡车与4辆可载
型卡车与4辆可载![]() 的
的![]() 型卡车,有9名驾驶员,建筑某段高速公路中,此公司承包了每天至少搬运
型卡车,有9名驾驶员,建筑某段高速公路中,此公司承包了每天至少搬运![]() 沥青的任务,已知每辆卡车每天往返的次数为
沥青的任务,已知每辆卡车每天往返的次数为![]() 型车8次,
型车8次, ![]() 型车6次,每辆卡车每天往返的成本费为
型车6次,每辆卡车每天往返的成本费为![]() 型车160元,
型车160元, ![]() 型车252元,每天派出
型车252元,每天派出![]() 型车和
型车和![]() 型车各多少辆,公司所花的成本费最低?
型车各多少辆,公司所花的成本费最低?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在四棱锥P﹣ABCD中,PA⊥底面ABCD,AC⊥AB,AD⊥DC,∠DAC=60°,PA=AC=2,AB=1. 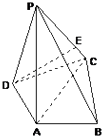
(1)求二面角A﹣PB﹣C的余弦值.
(2)在线段CP上是否存在一点E,使得DE⊥PB,若存在,求线段CE的长度,不存在,说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图所示,在正方体![]() 中,点
中,点![]() 是棱
是棱![]() 上的一个动点,平面
上的一个动点,平面![]() 交棱
交棱![]() 于点
于点![]() .给出下列命题:
.给出下列命题:
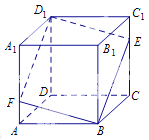
①存在点![]() ,使得
,使得![]() //平面
//平面![]() ;
;
②对于任意的点![]() ,平面
,平面![]() 平面
平面![]() ;
;
③存在点![]() ,使得
,使得![]() 平面
平面![]() ;
;
④对于任意的点![]() ,四棱锥
,四棱锥![]() 的体积均不变.
的体积均不变.
其中正确命题的序号是______.(写出所有正确命题的序号).
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设双曲线C的中心为点O,若有且只有一对相交于点O,所成的角为60°的直线A1B1和A2B2,使| A1B1|=| A2B2|,其中A1,B1和A2,B2分别是这对直线与双曲线C的交点,则该双曲线的离心率的取值范围是( )
A. (![]() ,2] B. [
,2] B. [![]() ,2) C. (
,2) C. (![]() ,+
,+![]() ) D. [
) D. [![]() ,+
,+![]() )
)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com