
(2006
全国I,22)设数列 的前n项的和
的前n项的和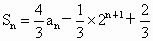 ,n=1,2,3,….
,n=1,2,3,….
(1)
求首项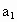 与通项
与通项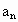 ;
;
(2)
设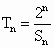 ,n=1,2,3,…,证明:
,n=1,2,3,…,证明: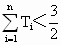 .
.  阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:013
(2006
全国Ⅰ,9)设平面向量 、
、 、
、 的和
的和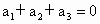 .如果平面向量
.如果平面向量 、
、 、
、 满足
满足 ,且
,且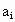 顺时针旋转30°后与
顺时针旋转30°后与 同向,其中i=1、2、3,则
同向,其中i=1、2、3,则
[
]|
A . |
B . |
|
C . |
D . |
查看答案和解析>>
科目:高中数学 来源: 题型:013
(2006
全国I,11)用长度分别为2、3、4、5、6(单位:cm)的5根细木棒围成一个三角形(允许连接,但不允许折断),能够得到的三角形的最大面积为[
]|
A . |
B . |
C . |
D . |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com