
【题目】已知函数f(x)=bax , (其中a,b为常数且a>0,a≠1)的图象经过点A(1,8),B(3,32)
(1)求f(x)的解析式;
(2)若不等式![]() +1﹣2m≥0在x∈(﹣∞,1]上恒成立,求实数m的取值范围.
+1﹣2m≥0在x∈(﹣∞,1]上恒成立,求实数m的取值范围.
【答案】解:(1)把点A(1,8),B(3,32)代入函数f(x)=bax , 可得![]() ,求得
,求得![]() ,∴f(x)=42x .
,∴f(x)=42x .
(2)不等式![]() +1﹣2m≥0,即 m≤
+1﹣2m≥0,即 m≤![]() [
[![]() ]2+
]2+![]()
![]() +
+![]() .
.
令t=![]() ,则 m≤
,则 m≤![]() t2+
t2+![]() t+
t+![]() .
.
记g(t)=![]() t2+
t2+![]() t+
t+![]() =
=![]() (t+
(t+![]() )2+
)2+![]() ,由x∈(﹣∞,1],可得t≥
,由x∈(﹣∞,1],可得t≥![]() .
.
故当t=![]() 时,函数g(t)取得最小值为
时,函数g(t)取得最小值为![]() .
.
由题意可得,m≤g(t)min , ∴m≤![]() .
.
【解析】(1)把点A(1,8),B(3,32)代入函数f(x)=bax , 求得a、b的值,可得f(x)的解析式.
(2)不等式即 m≤![]() [
[![]() ]2+
]2+![]()
![]() +
+![]() , 令t=
, 令t=![]() , 则 m≤
, 则 m≤![]() t2+
t2+![]() t+
t+![]() . 利用二次函数的性质求得g(t)=
. 利用二次函数的性质求得g(t)=![]() t2+
t2+![]() t+
t+![]() 的最小值,可得m的范围.
的最小值,可得m的范围.


 导学与测试系列答案
导学与测试系列答案 新非凡教辅冲刺100分系列答案
新非凡教辅冲刺100分系列答案科目:高中数学 来源: 题型:
【题目】如图,ABCD﹣A1B1C1D1是正方体,E,F,G,H,M,N分别是所在棱的中点,则下列结论错误的有
①GH和MN是平行直线;GH和EF是相交直线
②GH和MN是平行直线;MN和EF是相交直线
③GH和MN是相交直线;GH和EF是异面直线
④GH和EF是异面直线;MN和EF也是异面直线.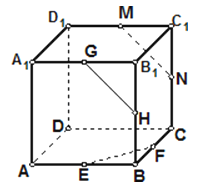
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知定点O(0,0),A(3,0),动点P到定点O距离与到定点A的距离的比值是![]() .
.
(Ⅰ)求动点P的轨迹方程,并说明方程表示的曲线;
(Ⅱ)当λ=4时,记动点P的轨迹为曲线D.F,G是曲线D上不同的两点,对于定点Q(﹣3,0),有|QF||QG|=4.试问无论F,G两点的位置怎样,直线FG能恒和一个定圆相切吗?若能,求出这个定圆的方程;若不能,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某中学将100名高二文科生分成水平相同的甲、乙两个“平行班”,每班50人.陈老师采用A,B两种不同的教学方式分别在甲、乙两个班进行教改实验.为了了解教学效果,期末考试后,陈老师对甲、乙两个班级的学生成绩进行统计分析,画出频率分布直方图(如下图).记成绩不低于90分者为“成绩优秀”.
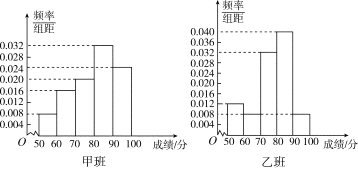
(Ⅰ)根据频率分布直方图填写下面2×2列联表;
甲班(A方式) | 乙班(B方式) | 总计 | |
成绩优秀 | |||
成绩不优秀 | |||
总计 |
(Ⅱ)判断能否在犯错误的概率不超过0.05的前提下认为:“成绩优秀”与教学方式有关?
附:![]() .
.
P(K2≥k) | 0.25 | 0.15 | 0.10 | 0.05 | 0.025 |
k | 1.323 | 2.072 | 2.706 | 3.841 | 5.024 |
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】若函数y=f(x)同时满足:(ⅰ)对于定义域内的任意x,恒有f(x)+f(﹣x)=0;(ⅱ)对于定义域内的任意x1 , x2 , 当x1≠x2时,恒有![]() , 则称函数f(x)为“二维函数”.现给出下列四个函数:
, 则称函数f(x)为“二维函数”.现给出下列四个函数:
①f(x)=![]()
②f(x)=﹣x3+x
③![]()
④![]()
其中能被称为“二维函数”的有 (写出所有满足条件的函数的序号).
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com