练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    【题目】如图，三棱锥中，平面，，，点，分别为，的中点.

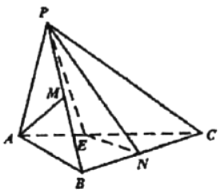
    (1)求证：平面；

    (2)是线段上的点，且平面.

    ①确定点的位置；

    ②求直线与平面所成角的正弦值.

    【答案】(1)证明见解析；(2)①为靠近的的一个三等分点；②.

    【解析】

    （1）由已知条件可证，即可证明结论；

    （2）①连结，交于，则是的重心，根据线面平行的性质定理，可证，结合重心的性质，即可确定点位置；

    ②作于，有，从而有平面，得到是直线与平面所成的角，解直角，即可得出结论.

    (1)，为中点，，

    平面，平面，

    ，平面.

    (2)①连结，交于，则是的重心，

    且，平面，平面，

    平面平面，

    ，，

    即为靠近的的一个三等分点.

    ②作于，则，平面，

    是直线与平面所成的角，

    且，，

    ，

    ，

    ，

    直线与平面所成角的正弦值是.

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

    【题目】已知抛物线 ，其焦点到准线的距离为2，直线与抛物线交于，两点，过，分别作抛物线的切线，，与交于点.

    （Ⅰ）求的值；

    （Ⅱ）若，求面积的最小值.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】如图，圆，是圆M内一个定点，P是圆上任意一点，线段PN的垂直平分线l和半径MP相交于点Q，当点P在圆M上运动时，点Q的轨迹为曲线E.

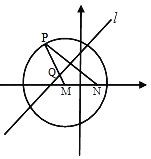
    （1）求曲线E的方程；

    （2）已知抛物线上，是否存在直线m与曲线E交于G，H，使得G，H中点F落在直线y＝2x上，并且与抛物线相切，若直线m存在，求出直线m的方程，若不存在，说明理由.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】在四棱柱中，，且，平面，.

    （1）证明：.

    （2）求与平面所成角的正弦值.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知的顶点，边上的中线所在直线方程为，的角平分线所在直线方程为．

    （I）求顶点的坐标；

    （II）求直线的方程．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】某大型超市公司计划在市新城区开设分店，为确定在新城区开设分店的个数，该公司对该市已开设分店的其他区的数据统计后得到下列信息（其中表示在该区开设分店的个数，表示这个分店的年收入之和）：

    分店个数（个）

    2

    3

    4

    5

    6

    年收入（万元）

    250

    300

    400

    450

    600

    （Ⅰ）该公司经过初步判断，可用线性回归模型拟合与的关系，求关于的回归方程；

    （Ⅱ）假设该公司每年在新城区获得的总利润（单位：万元）与，之间的关系为，请根据（Ⅰ）中的线性回归方程，估算该公司在新城区开设多少个分店时，才能使新城区每年每个分店的平均利润最大.

    参考公式：回归方程中斜率和截距的最小二乘估计公式分别为： ，.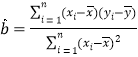

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知函数，．

    （1）若直线与函数的图象相切，求实数的值；

    （2）若存在，，使，且，求实数的取值范围；

    （3）当时，求证：．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】如图所示,已知点是抛物线上一定点,直线的倾斜角互补,且与抛物线另交于，两个不同的点．

    (1)求点到其准线的距离；

    (2)求证：直线的斜率为定值．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】在如图所示的空间几何体中，平面平面与都是边长为2的等边三角形，与平面所成的角为60°，且点在平面上的射影落在的平分线上.

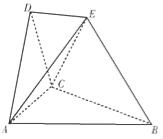
    （1）求证：平面；

    (2)求四面体的体积.

    查看答案和解析>>

    同步练习册答案