
【题目】定义:在数列{an}中,若an2﹣an﹣12=p,(n≥2,n∈N* , p为常数),则称{an}为“等方差数列”,下列是对“等方差数列”的有关判断:
①若{an}是“等方差数列”,则数列{ ![]() }是等差数列;
}是等差数列;
②{(﹣2)n}是“等方差数列”;
③若{an}是“等方差数列”,则数列{akn}(k∈N* , k为常数)也是“等方差数列”;
④若{an}既是“等方差数列”,又是等差数列,则该数列是常数数列.
其中正确命题的个数为( )
A.1
B.2
C.3
D.4
【答案】B
【解析】解:根据题意,依次分析四个判断:①、若{an}是“等方差数列”,假设an= ![]() ,则
,则 ![]() =
= ![]() ,不是等差数列,则①错误;②:对数列{(﹣2)n}有an2﹣an﹣12=[(﹣2)n]2﹣[(﹣2)n﹣1]2=4n﹣4n﹣1不是常数,所以②错误③:对数列{akn}有akn2﹣ak(n﹣1)2=(akn2﹣akn﹣12)+(akn﹣12﹣akn﹣22)+…+(akn﹣k+12﹣akn﹣k2)=kp,而k,p均为常数,所以数列{akn}也是“等方差数列”,所以③正确④:设数列{an}首项a1,公差为d则有a2=a1+d,a3=a1+2d,所以有(a1+d)2﹣a12=p,且(a1+2d)2﹣(a1+d)2=p,所以得d2+2a1d=p,3d2+2a1d=p,上两式相减得d=0,所以此数列为常数数列,所以④正确.
,不是等差数列,则①错误;②:对数列{(﹣2)n}有an2﹣an﹣12=[(﹣2)n]2﹣[(﹣2)n﹣1]2=4n﹣4n﹣1不是常数,所以②错误③:对数列{akn}有akn2﹣ak(n﹣1)2=(akn2﹣akn﹣12)+(akn﹣12﹣akn﹣22)+…+(akn﹣k+12﹣akn﹣k2)=kp,而k,p均为常数,所以数列{akn}也是“等方差数列”,所以③正确④:设数列{an}首项a1,公差为d则有a2=a1+d,a3=a1+2d,所以有(a1+d)2﹣a12=p,且(a1+2d)2﹣(a1+d)2=p,所以得d2+2a1d=p,3d2+2a1d=p,上两式相减得d=0,所以此数列为常数数列,所以④正确.
有2个正确;
所以答案是:B.
【考点精析】通过灵活运用数列的通项公式,掌握如果数列an的第n项与n之间的关系可以用一个公式表示,那么这个公式就叫这个数列的通项公式即可以解答此题.


 期末1卷素质教育评估卷系列答案
期末1卷素质教育评估卷系列答案科目:高中数学 来源: 题型:
【题目】某公司为对本公司的160名员工的身体状况进行调查,先将员工随机编号为1,2,3,…,159,160,采用系统抽样的方法(等间距地抽取,每段抽取一个个体)将抽取的一个样本.已知抽取的员工中最小的两个编号为5,21,那么抽取的员工中,最大的编号应该是( )
A.141
B.142
C.149
D.150
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=x﹣alnx(a∈R)
(1)当a=2时,求曲线y=f(x)在点A(1,f(1))处的切线方程;
(2)求函数f(x)的极值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】等比数列{an}中,已知a1=2,a4=16.
(1)求数列{an}的通项公式an;
(2)若a3 , a5分别是等差数列{bn}的第4项和第16项,求数列{bn}的通项公式及前n项和Sn .
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知数列{an}中,a1=1,a1+2a2+3a3+…+nan= ![]() (n≥1,n∈Z)
(n≥1,n∈Z)
(1)求数列{an}的通项公式an;
(2)求数列{n2an}的前n项和Tn .
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设f(n)=(1+ ![]() )n﹣n,其中n为正整数.
)n﹣n,其中n为正整数.
(1)求f(1),f(2),f(3)的值;
(2)猜想满足不等式f(n)<0的正整数n的范围,并用数学归纳法证明你的猜想.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如果圆(x﹣a)2+(y﹣a)2=8上总存在到原点的距离为 ![]() 的点,则实数a的取值范围是( )
的点,则实数a的取值范围是( )
A.(﹣3,﹣1)∪(1,3)
B.(﹣3,3)
C.[﹣1,1]
D.[﹣3,﹣1]∪[1,3]
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知正项数列{an}的前n项和为Sn , 若{an}和 ![]() 都是等差数列,且公差相等.
都是等差数列,且公差相等.
(1)求数列{an}的通项公式;
(2)令bn= ![]() ,cn=bnbn+1 , 求数列{cn}的前n项和Tn .
,cn=bnbn+1 , 求数列{cn}的前n项和Tn .
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,一个树形图依据下列规律不断生长:1个空心圆点到下一行仅生长出1个实心圆点,1个实心圆点到下一行生长出1个实心圆点和1个空心圆点.则第11行的实心圆点的个数是 . 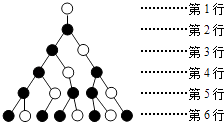
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com