
【题目】![]() 中,
中,![]() 为
为![]() 的中点,
的中点,![]() 为外心,点
为外心,点![]() 满足
满足![]() .
.
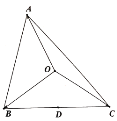
(1)证明:![]() ;
;
(2)若![]() ,设
,设![]() 与
与![]() 相交于点
相交于点![]() ,
,![]() 关于点
关于点![]() 对称,且
对称,且![]() ,求
,求![]() 的取值范围.
的取值范围.
 作业辅导系列答案
作业辅导系列答案 同步学典一课多练系列答案
同步学典一课多练系列答案 经典密卷系列答案
经典密卷系列答案 金牌课堂练系列答案
金牌课堂练系列答案科目:高中数学 来源: 题型:
【题目】如图,马路![]() 南边有一小池塘,池塘岸
南边有一小池塘,池塘岸![]() 长40米,池塘的最远端
长40米,池塘的最远端![]() 到
到![]() 的距离为400米,且池塘的边界为抛物线型,现要在池塘的周边建一个等腰梯形的环池塘小路
的距离为400米,且池塘的边界为抛物线型,现要在池塘的周边建一个等腰梯形的环池塘小路![]() ,且
,且![]() 均与小池塘岸线相切,记
均与小池塘岸线相切,记![]() .
.

(1)求小路的总长,用![]() 表示;
表示;
(2)若在小路与小池塘之间(图中阴影区域)铺上草坪,求所需铺草坪面积最小时,![]() 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某企业生产A、B两种产品,生产每一吨产品所需的劳动力和煤、电耗如下表:
产品品种 | 劳动力 | 煤 | 电 |
A产品 | 3 | 9 | 4 |
B产品 | 10 | 4 | 5 |
已知生产每吨A产品的利润是7万元,生产每吨B产品的利润是12万元,现在条件有限,该企业仅有劳动力300个,煤360吨,并且供电局只能供电200千瓦,试问:该企业生产A、B两种产品各多少吨,才能获得最大利润?并求出最大利润.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() ,
,![]() .
.
(1)若函数![]() 在区间
在区间![]() 上的最大值和最小值之和为6,求实数
上的最大值和最小值之和为6,求实数![]() 的值;
的值;
(2)设函数![]() ,若函数
,若函数![]() 在区间
在区间![]() 上恒有零点,求实数
上恒有零点,求实数![]() 的取值范围;
的取值范围;
(3)在问题(2)中,令![]() ,比较
,比较![]() 与0的大小关系,并说明理由.
与0的大小关系,并说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】一片森林原面积为![]() ,计划从某年开始,每年砍伐一些树林,且每年砍伐面积与上一年剩余面积的百分比相等.并计划砍伐到原面积的一半时,所用时间是10年.为保护生态环境,森林面积至少要保留原面积的
,计划从某年开始,每年砍伐一些树林,且每年砍伐面积与上一年剩余面积的百分比相等.并计划砍伐到原面积的一半时,所用时间是10年.为保护生态环境,森林面积至少要保留原面积的![]() .已知到今年为止,森林剩余面积为原面积的
.已知到今年为止,森林剩余面积为原面积的![]() .
.
(1)求每年砍伐面积与上一年剩余面积的百分比;
(2)到今年为止,该森林已砍伐了多少年?
(3)为保护生态环境,今后最多还能砍伐多少年?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】中国古代数学著作《算法统综》中有这样一个问题:“三百七十八里关,初步健步不为难,次日脚痛减一半,六朝才得到其关,要见次日行里数,请公仔细算相还”其大意为:“有一个人走378里路,第一天健步走,从第二天起因脚痛每天走的路程为前一天的一半,走了6天后到达目的地”,请问此人第5天走的路程为( )
A. 36里 B. 24里 C. 18里 D. 12里
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】函数y = f(x)是定义域为R的偶函数,当x≥0时,函数f(x)的图象是由一段抛物线和一条射线组成(如图所示).

①当![]() 时,y的取值范围是______;
时,y的取值范围是______;
②如果对任意![]() (b <0),都有
(b <0),都有![]() ,那么b的最大值是______.
,那么b的最大值是______.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com