
【题目】已知函数![]() .
.
(Ⅰ) 当a=0时,求曲线f(x)在x =1处的切线方程;
(Ⅱ) 设函数![]() ,求函数h(x)的极值;
,求函数h(x)的极值;
(Ⅲ) 若![]() 在[1,e](e=2.718 28…)上存在一点x0,使得
在[1,e](e=2.718 28…)上存在一点x0,使得![]() 成立,求a的取值范围.
成立,求a的取值范围.
【答案】(Ⅰ)切线方程为![]() ;
;
(Ⅱ)当![]() 时,
时, ![]() 在
在![]() 处取得极大值
处取得极大值![]()
![]() ,无极小值;当
,无极小值;当![]() 时,
时, ![]() 在区间
在区间![]() 上无极值;
上无极值;
(Ⅲ)![]() 或
或![]()
【解析】试题分析:(Ⅰ)求出函数的导数,计算![]() ,根据点斜式即可求出切线方程;(Ⅱ)求出
,根据点斜式即可求出切线方程;(Ⅱ)求出![]() 的导数,通过讨论
的导数,通过讨论![]() 的范围,利用导数求出函数的单调区间,从而求出函数的极值即可;(Ⅲ)问题转化为函数
的范围,利用导数求出函数的单调区间,从而求出函数的极值即可;(Ⅲ)问题转化为函数![]() 在
在![]() 上,有
上,有![]() ,通过讨论
,通过讨论![]() 的范围,得到函数的单调性,从而求出
的范围,得到函数的单调性,从而求出![]() 的范围即可.
的范围即可.
试题解析:(Ⅰ) 当a=0时,f (x) =![]() , f (1) =1, 则切点为(1, 1),分
, f (1) =1, 则切点为(1, 1),分
∵![]() , ∴切线的斜率为
, ∴切线的斜率为![]() ,
,
∴曲线f (x)在点(1, 1)处的切线方程为y1= ( x1),即x+ y2=0
(Ⅱ)依题意![]() ,定义域为(0, +∞),
,定义域为(0, +∞),
∴![]() ,
,
①当a+1>0,即a>1时,令![]() ,∵x>0,∴0<x<1+ a,
,∵x>0,∴0<x<1+ a,
此时,h(x) 在区间(0, a+1)上单调递增,
令![]() ,得 x>1+ a.
,得 x>1+ a.
此时,h(x)在区间(a+1,+∞)上单调递减.
②当a+1≤0,即a≤1时, ![]() 恒成立, h(x)在区间(0,+∞)上单调递减.
恒成立, h(x)在区间(0,+∞)上单调递减.
综上,当a>1时,h(x)在x=1+a处取得极大值h(1+a)=![]() ,无极小值;
,无极小值;
当a≤1时,h(x)在区间(0,+∞)上无极值.
(Ⅲ) 依题意知,在[1, e]上存在一点x0,使得![]() 成立,
成立,
即在[1, e]上存在一点x0,使得h(x0)≥0,
故函数![]() 在[1, e]上,有h(x)max≥0.
在[1, e]上,有h(x)max≥0.
由(Ⅱ)可知,①当a+1≥e, 即a≥e1时,h(x)在[1, e]上单调递增,
∴![]() , ∴
, ∴![]() ,
,
∵![]() ,∴
,∴![]() .
.
②当0<a+1≤1,或a≤1,即a≤0时,h(x)在[1, e]上单调递减,
∴![]() ,∴a ≤2.
,∴a ≤2.
③当1<a+1<e,即0<a<e1时,
由(Ⅱ)可知,h(x)在x=1+a处取得极大值也是区间(0, +∞)上的最大值,
即h(x)max=h(1+a)=![]() ,
,
∵0<ln(a+1)<1, ∴h(1+a)<0在[1, e]上恒成立,
此时不存在x0使h(x0)≥0成立.
综上可得,所求a的取值范围是![]() 或a≤2.
或a≤2.
【方法点晴】本题主要考查利用导数求曲线切线以及利用导数研究函数的单调性及极值值,属于难题.求曲线切线方程的一般步骤是:(1)求出![]() 在
在![]() 处的导数,即
处的导数,即![]() 在点
在点![]()
![]() 出的切线斜率(当曲线
出的切线斜率(当曲线![]() 在
在![]() 处的切线与
处的切线与![]() 轴平行时,在 处导数不存在,切线方程为
轴平行时,在 处导数不存在,切线方程为![]() );(2)由点斜式求得切线方程
);(2)由点斜式求得切线方程![]() .
.


科目:高中数学 来源: 题型:
【题目】如图,在四棱锥![]() 中,
中, ![]() ,
, ![]() 平面
平面![]() ,
, ![]() .
.
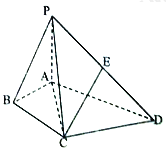
(1)设点![]() 为
为![]() 的中点,求证:
的中点,求证: ![]() 平面
平面![]() ;
;
(2)线段![]() 上是否存在一点
上是否存在一点![]() ,使得直线
,使得直线![]() 与平面
与平面![]() 所成的角
所成的角![]() 的正弦值为
的正弦值为![]() ?若存在,试确定点
?若存在,试确定点![]() 的位置;若不存在,请说明理由.
的位置;若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】选修4-4:坐标系与参数方程
在直角坐标系![]() 中,直线
中,直线![]() 的参数方程为
的参数方程为![]() (
(![]() 为参数),在极坐标系(与直角坐标系
为参数),在极坐标系(与直角坐标系![]() 取相同的长度单位,且以原点
取相同的长度单位,且以原点![]() 为极点,以
为极点,以![]() 轴正半轴为极轴)中,圆
轴正半轴为极轴)中,圆![]() 的方程为
的方程为![]() .
.
(1)求圆![]() 的直角坐标方程;
的直角坐标方程;
(2)设圆![]() 与直线
与直线![]() 交于点
交于点![]() ,若点
,若点![]() 的坐标为
的坐标为![]() ,求
,求![]() 的最小值.
的最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=x2+bx+c,(b,c∈R),集合A={x丨f(x)=0},B={x|f(f(x))=0},若存在x0∈B,x0A则实数b的取值范围是( )
A.b≠0
B.b<0或b≥4
C.0≤b<4
D.b≤4或b≥4
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】选修4-4:坐标系与参数方程
在直角坐标系![]() 中,直线
中,直线![]() 的倾斜角为
的倾斜角为![]() 且经过点
且经过点![]() ,以原点
,以原点![]() 为极点,以
为极点,以![]() 轴正半轴为极轴,与直角坐标系
轴正半轴为极轴,与直角坐标系![]() 取相同的长度单位,建立极坐标系,设曲线
取相同的长度单位,建立极坐标系,设曲线![]() 的极坐标方程为
的极坐标方程为![]() .
.
(1)若直线![]() 与曲线
与曲线![]() 有公共点,求
有公共点,求![]() 的取值范围;
的取值范围;
(2)设![]() 为曲线
为曲线![]() 上任意一点,求
上任意一点,求![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】广东某市一玩具厂生产一种玩具深受大家喜欢,经市场调查该商品每月的销售量![]() (单位:千件)与销售价格
(单位:千件)与销售价格![]() (单位:元/件)满足关系式
(单位:元/件)满足关系式![]() ,其中
,其中![]() ,
, ![]() 为常数.已知销售价格为4元/件时,每日可售出玩具21千件.
为常数.已知销售价格为4元/件时,每日可售出玩具21千件.
(1)求![]() 的值;
的值;
(2)假设该厂生产这种玩具的成本、员工工资等所有开销折合为每件2元(只考虑销售出的件数),试确定销售价格![]() 的值,使该厂每日销售这种玩具所获得的利润最大.(保留1位小数)
的值,使该厂每日销售这种玩具所获得的利润最大.(保留1位小数)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图所示,在四棱锥![]() 中,
中, ![]() 平面
平面![]() ,底面
,底面![]() 是菱形,
是菱形, ![]() ,
, ![]() ,
, ![]() .
. ![]() 为
为![]() 与
与![]() 的交点,
的交点, ![]() 为棱
为棱![]() 上一点,
上一点,
(1)证明:平面![]() ⊥平面
⊥平面![]() ;
;
(2)若三棱锥![]() 的体积为
的体积为![]() ,
,
求证: ![]() ∥平面
∥平面![]() .
.

查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,关于正方体ABCD﹣A1B1C1D1 , 下面结论错误的是( ) 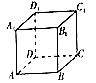
A.BD⊥平面ACC1A1
B.AC⊥BD
C.A1B∥平面CDD1C1
D.该正方体的外接球和内接球的半径之比为2:1
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com