练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    【题目】定义“等积数列”，在一个数列中，如果每一项与它的后一项的积都为同一个常数，那么这个数列叫做等积数列，这个常数叫做该数列的公积，已知数列{an}是等积数列且a1=2，公积为10，那么这个数列前21项和S21的值为_____________.

    【答案】72

    【解析】

    由等积数列的定义，可得a1=2，a2=5，a3=2，a4=5，…，即为周期为2的数列，即可得到数列前21项和．

    数列{an}是等积数列且a1=2，公积为10，

    可得a2=5，a3=2，a4=5，…，

    则前21项和S21=2+5+2+5+…+2=7×10+2=72．

    故答案为：72．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

    【题目】

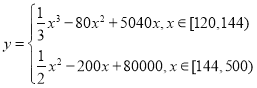    为了保护环境，发展低碳经济，某单位在政府部门的支持下，进行技术攻关，采用了新工艺，新上了把二氧化碳转化为一种可利用的化工产品的项目.经测算，月处理成本（元）与月处理量（吨）之间的函数关系可以近似的表示为：，且每处理一吨二氧化碳可得到能利用的化工产品价值为200元，若该项目不获利，政府将补贴.

    （I）当时，判断该项目能否获利？如果获利，求出最大利润；如果不获利，则政府每月至少需要补贴多少元才能使该项目不亏损；

    （II）该项目每月处理量为多少吨时，才能使每吨的平均处理成本最低？

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】下列说法中正确的是（ ）

    A．统计方法的特点是统计推断准确、有效

    B．独立性检验的基本思想类似于数学中的反证法

    C．任何两个分类变量有关系的可信度都可以通过查表得到

    D．不能从等高条形图中看出两个分类变量是否相关

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】某城市响应城市绿化的号召， 计划建一个如图所示的三角形形状的主题公园,其中一边利用现成的围墙，长度为米，另外两边使用某种新型材料围成，已知单位均为米）．

    （1）求满足的关系式（指出的取值范围）；

    （2）在保证围成的是三角形公园的情况下，如何设计能使所用的新型材料总长度最短？最短长度是多少？

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】命题“若x2<1,则-1<x<1”的逆否命题是( )

    A. 若x2≥1,则x≥1或x≤-1. B. 若-1<x<1,则x2<1

    C. 若x≥1且x≤-1,则x2≥1 D. 若x≥1或x≤-1,则x2≥1

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知等差数列{}满足： ＝2，且成等比数列.

    (1）求数列{}的通项公式.

    (2）记为数列{}的前n项和，是否存在正整数n，使得？若存在，求n的最小值；若不存在，说明理由.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】直线x－y＝0的倾斜角为___________

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】用辗转相除法求72与120的最大公约数时，需要做除法次数为(　　)

    A. 4 B. 3 C. 5 D. 6

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】下面是一个2×2列联表：

    y1

    y2

    总计

    x1

    a

    26

    78

    x2

    8

    25

    33

    总计

    b

    51

    c

    则表中a，b处的值分别为(　　)

    A. 94，96 B. 52，50 C. 52，60 D. 54，52

    查看答案和解析>>

    同步练习册答案